方法1 2のうち方法1：重複しない組み合わせで計算する。

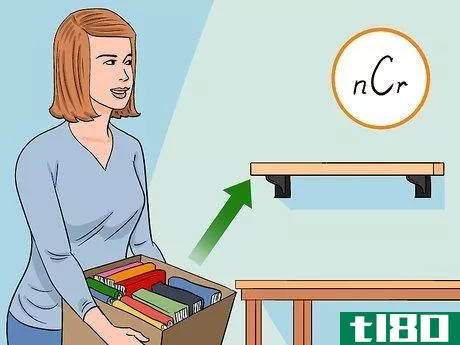
1. 1 順番は重要でなく、繰り返しも許されない例題を考えてみましょう。例えば、10冊の本があり、そのうちの6冊を棚に並べる方法の数を調べたいとします。この場合、順番は気にせず、どの本を一度だけ使うとして、どのグループ分けで表示できるかを知りたいだけなのです。このような問題は通常、nCr{displaystyle {}_{n}C_{r}}, C(n,r){displaystyle C(n,r)}, (nr){displaystyle {binom {n}{r}}, または "n selects r" というラベルで表示されます。これらの記号において、n{displaystyle n}は選択したい項目（自分のサンプル）の数、r{displaystyle r}は選択したい項目の数である。

2. 2は次の式を知っている：nCr=n!(n-r)!r!{}_{n}C_{r}={frac {n!}{(n-r)!r!}}.この式は順列の式と似ていますが、同じではありません。nPr = n!(n-r) として使用することができます!{}_{n}P_{r}={frac {n!}{(n-r)!}} とする。組み合わせを求めよ }}。組み合わせの式は、順番が関係なくなるので少し違います。そのため、順列の式をn！{displaystyle n！}で割って冗長性をなくします。本来は、異なる順列であっても同じと考えられる選択肢の数だけ結果を減らしているのです（組み合わせに順序は関係ないため）。
3. 3 n{displaystyle n}とr{displaystyle r}に値を入力します。上記の場合、nCr=10!(10-6)!6!{}displaystyle {}_{n}C_{r}={prac {10!}{(10-6)!6!}} という式が得られます。nCr=10!(4!)(6!){_{n}C_{r}={frac {10!}{(4!)(6!)}} に簡略化されるでしょう。
4. 4.方程式を解いて、組み合わせの数を求めます。手書きでも電卓でも構いません。電卓をお持ちの方は、階乗の設定を見つけて、それを使って組み合わせの数を計算してみてください。Googleの電卓を使う場合は、必要な数字を入力したらその都度×！ボタンをクリックします。この例では、(10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1)を使って10！を計算し、3628800を得ます。24.6×5×4×3×2×1）を使って6！を求めると720となる。そして、この2つの数字を掛け合わせて合計個数を求める。この例では、24×720となり、17,280が分母となります。3,628,800/17,280。この例では、210となります。これは、本棚の本の組み合わせが210通りあり、重複はなく、順番は関係ないことを意味しています。

方法 2 の 2：組み合わせと繰り返しの計算

1. 1 順番は関係なく、繰り返しが許される問題の例を考えてみましょう。この種の問題では、同じアイテムを複数回使用することができます。例えば、15種類のメニューから5種類を選び、順番は気にせず、同じものを複数個注文する（＝リピートOK）場合を考えてみましょう。このような問題には、n+r-1Cr{displaystyle {}_{n+r-1}C_{r}} というラベルを付けることができます。通常、選択したい選択肢の数にはn{displaystyle n}、選択したい項目の数にはr{displaystyle r}を使用します。この種の問題では、繰り返しが許され、順番は関係ないことを覚えておいてください。これは最も一般的でなく、最も理解されていない組み合わせや交換のタイプであり、一般的にはあまり教えられない。これが関係している場合、K-selection、K-multigroup、K-combination with repetitionとも呼ばれることが多い。
2. 2 式を知っている：n+r-1Cr=(n+r-1)!(n-1)!r!{{n+r-1}C_{r}={{frac {(n+r-1)!}(n-1)!r!}}となる。
3. 3 n{displaystyle n}とr{displaystyle r}に値を入力します。この例では、n+r-1Cr=(15+5-1)という式になる!(15-1)!5!{}_{n+r-1}C_{r}={{frac {(15+5-1)!}} {}_displaystyle {}_{n+r-1}C_{r{(15-1)!5!}n+r-1Cr=19!(14!)(5!) {}_{n+r-1}C_{r}={frac {19!}{(14!)(5!) }}に簡略化される。
4. 4.方程式を解いて、組み合わせの数を求めます。手書きでも電卓でも構いません。電卓をお持ちの方は、階乗の設定を見つけて、それを使って組み合わせの数を計算してみてください。Googleの電卓を使う場合は、必要な数値を入力するたびに×！ボタンをクリックします。もし、手で解かなければならない場合は、それぞれの階乗について、与えられた主要な数から始めて、次に小さい数を掛け、0になるまで続けることを覚えておいてください。メニューの15品目から、任意の5品目を注文する方法は、順番は関係なく、繰り返しが許される11628通りもあります。

• グラフ電卓の中には、組み合わせを繰り返し解くことなく、素早く解けるようにするためのボタンが用意されているものもあります。このボタンがある電卓では、まず n{displaystyle n} の値を入力し、次にコンビネーションボタン、そして r{displaystyle r} の値を入力してください。