方法1 2の方法1：標本分散の計算

1. 1 部分的なデータセットを扱う場合は、標本分散の公式を使用します。ほとんどの場合、統計学者が入手できるのは1つの標本、つまり研究対象の母集団のサブセットのみです。例えば、「ドイツにおける自動車1台あたりのコスト」を分析する代わりに、統計学者が数千台の自動車を無作為に抽出した場合のコストを求めることができるのです。このサンプルを使って、ドイツでの自動車購入費用の見積もりを取ることはできるが、実際の数字とは正確に一致しない可能性が高い。例食堂で1日に売られるマフィンの数を分析するために、6日間の無作為抽出をしたところ、次のような結果が得られました。 38, 37, 36, 28, 18, 14, 12, 11, 10.7, 9.9. 食堂の各日のデータがないため、これは母数ではなくサンプルです。母集団のすべてのデータポイントがある場合は、以下の方法にスキップすることができます。

2. 2 標本分散の公式を書きなさい。データセットの分散は、データポイントがどのように分布しているかを教えてくれる。分散がゼロに近いほど、データポイントがより密接にクラスタリングされていることを意味する。サンプルデータセットを扱うときは、次の式を使って分散を計算する：s2{displaystyle s^{2}} = ∑[(xi{displaystyle x_{i} - x̅)2{displaystyle ^{2}}]/(n - 1)s2{displaystyle s^{2}} は分散である．xi{displaystyle x_{i}}はデータセット内の項目を表します。合計」を意味する∑は、xi{displaystyle x_{i}}の各値について以下の項を計算し、それらを足すことを指示します。 x̅はサンプルの平均です。

3. 3 標本の平均を計算する。記号x̅または "x-bar "はサンプルの平均を意味する。すべてのデータポイントを合計し、データポイントの数で割るという、他の平均と同じように計算する。例17 + 15 + 23 + 7 + 9 + 13 = 84 次に、答えをデータポイントの数（この場合は6）で割ります。データが平均値の周りに集まっていれば、分散は小さい。データが平均から遠く離れて散らばっている場合、分散は大きくなります。

4. 4 各データポイントから平均値を差し引く。さて、いよいよxi{displaystyle x_{i}}の計算です。- x̅で、xi{displaystyle x_{i}}はデータセットの各数値です。それぞれの答えは、その数字が平均からどれくらい乖離しているか、わかりやすく言えば「平均からどれくらい離れているか」を示しているのです。例：x1{displaystyle x_{1}}。- x̅ = 17 - 14 = 3x2{displaystyleのx_{2}}。- x̅ = 15 - 14 = 1x3{displaystyleのx_{3}}です。- x̅ = 23 - 14 = 9x4{displaystyle x_{4}}となる。- x̅ = 7 - 14 = -7x5{displaystyle x_{5}} x̅ = 9 - 14 = -7x5{displaystyle x_{5}} になります。- x̅ = 9 - 14 = -5x6{displaystyle x_{6}} x̅ = 13 - 14 = -1x6{displaystyle x_{6}}. x̅ = 13 - 14 = -5x6{displaystyle x_{6}} .- x̅ = 13 - 14 = -1 答えの足し算が0になるはずなので、確認は簡単です。これは、平均の定義によるもので、マイナスの答え（平均から小さい数までの距離）は、プラスの答え（平均から大きい数までの距離）を正確に打ち消すからである。

5. 5 スクエアの各結果。前述のように、現在の偏差値リストの和（xi{displaystyle x_{i}}-x̅）は0である。つまり、「平均偏差」も常にゼロになるので、これではデータの分布がよくわからない。この問題を解くには、各偏差値の2乗を求めます。そうすると、すべてプラスになるので、マイナスとプラスの値が打ち消しあってゼロになることはなくなります。例(x1{displaystyle x_{1}}-x̅)2=32{displaystyle ^{2}=3^{2}=9}(x2{displaystyle (x_{2}}-x̅)2=12{displaystyle ^{2}=1^{2}=1}92=81(-)7)2=)49(-5)2= 25(-1)2= 1 これでサンプルの各データ点の値 (xi{displaystyle x_{i}}-x̅)2{displaystyle ^{2} が揃いました。

6. 6 二乗した値の総和を求めます。ここで、式（1）の分子全体を計算することになる。∑[(xi{displaystyle x_{i}}-x̅)2{displaystyle ^{2}} ]となります。大文字のシグマ、∑は、xi{displaystyle x_{i}}の各値について、次の項の値を合計することを指示します。サンプル中のxi{displaystyle x_{i}}の各値について(xi{displaystyle x_{i}} - x̅)2{displaystyle ^{2}}をすでに計算しているので、あとはすべての2乗偏差の結果を合計するだけでいいのです。例：9+1+81+49+25+1=166。

7. 7 を n - 1 で割ったもので、n はデータ点の数である。一昔前，統計学者は標本の分散を計算するときに，単純にnで割っていました．この方法では，偏差の二乗の平均が得られ，それは標本の分散と正確に一致します．しかし、サンプルはより大きな母集団の推定値に過ぎないことを忘れないでください。もし、別の無作為のサンプルを取って同じ計算をしたら、違う結果が出るでしょう。nで割るよりもn-1で割った方が、より大きな母集団の分散をよりよく推定できることがわかりました。この補正は非常に一般的であり、現在では標本分散の定義として受け入れられている。例標本の分散 = s2 = 1666-1 = {displaystyle s^{2} = {frac {166}{6-1}}=}... 33.2

8. 8 分散と標準偏差を理解する。なお、式中に指数があるため、分散は元データの2乗単位で測定される。そのため、直感的に理解することが難しい場合があります。その代わり、標準偏差を使うのが便利なことが多い。標準偏差は分散の平方根と定義されているので、無駄な努力はしていないのですが。標本の分散がs2{{displaystyle s^{2}}と書かれ、標本の標準偏差がs{displaystyle s}と書かれるのはこのためです。｝例えば、上記のサンプルの標準偏差＝s＝√33.2＝5.76となる。

方法2 方法2：母集団の違いを計算する

1. 1 母集団の各点についてデータを収集した場合は、母集団の分散の公式を使用します。母集団 "という用語は、関連する観測の総セットを意味する。例えば、テキサス州の住民の年齢を調べる場合、母集団にはすべてのテキサス州住民の年齢が含まれることになります。通常、このような大きなデータは表計算ソフトで作成しますが、ここでは小さなデータの例を紹介します。例水族館の一室には、ちょうど6つの水槽があります。この6つの水槽の魚の数は、x1=5{表示形式 x_{1}=5} x2=5{表示形式 x_{2}=5} x3=8{表示形式 x_{3}=8} x4=12{表示形式 x_{4}=12} x5=15{表示形式 x_{5}=15} となります。displaystyle x_{5}=15}x6=18{displaystyle x_{6}=18}のようになります。

2. 2 母集団の分散の公式を書きなさい。母集団には必要なデータがすべて含まれているので、この式は母集団の正確な分散を与えてくれます。標本分散（単なる推定値）と区別するために，統計学者は別の変数を用いる：σ2{displaystyle ^{2}} = (∑(xi{displaystyle x_{i}}-μ)2{displaystyle ^{2}})/nσ2{displaystyle ^{2}} = 母分散.σ2{displaystyle}}は，母分散を表す．xi{displaystyle x_{i}} はデータセット中の項を表す。∑内の項は、xi{displaystyle x_{i}}の各値について計算し、合計することになります。

3. 3 母集団の平均を求めよ。母集団を分析する場合、μ（ミュー）という記号は算術平均を表します。平均を求めるには、すべてのデータポイントを足し合わせて、データポイントの数で割ります。平均は「平均」と考えてもよいが、数学ではこの言葉の定義が複数あるので注意が必要である。例：平均 = μ = 5+5+8+12+15+186{displaystyle {frac {5+5+8+12+15+18}{6}} = 10.5

4. 4 各データポイントから平均値を差し引く。平均に近いデータポイントは、差がゼロに近くなる。各データポイントについて引き算の問題を繰り返すと、データの分布が見えてくるかもしれません。例えば、x1{displaystyle x_{1}}の場合。- μ = 5 - 10.5 = -5.5x2{displaystyle x_{2}} μ = 5 - 10.5 = -5.5x2{displaystyle x_{2}}となる。- μ = 5 - 10.5 = -5.5x3{displaystyle x_{3}}となる。- μ = 8 - 10.5 = -2.5x4{displaystyle x_{4}}となります。- μ = 12 - 10.5 = 1.5x5{displaystyle x_{5}} - μ = 15 - 10.5 = 4.5x6{displaystyle x_{6}}。- μ = 18 - 10.5 = 7.5

5. 5 各回答を正方形にする。さて、前のステップで得た数値のうち、いくつかは負の数、いくつかは正の数であることがわかります。データを数直線上に描くと、この2種類の数字は、平均より左側の数字と平均より右側の数字を表します。これでは、2つのセットが互いに相殺されてしまうので、分散の計算には使えません。すべての数値が正になるように、それぞれの数値を二乗してください。例：(xi{displaystyle x_{i}}-μ)2{displaystyle ^{2}} 1から6までの各iの値に対して：(-5.5)2{displaystyle ^{2}} = 30.25(-5.5)2{displaystyle ^{2}} = 30.[-2.5]2{displaystyle^{2displaystyle ^{2}} = 6.25(1.5)2{displaystyle ^{2}} = 2.25(4.5)2{displaystyle ^{2}} = 20.25(7.5)2{displaystyle ^{2}} = 56.25を満たすこと。

6. 6 結果の平均を求めます。これで、各データポイントについて、そのデータポイントの平均からの距離に関連する値が（間接的に）得られたことになります。これらの値を足し合わせ、値の数で割って平均値を求めます。例えば，母集団の分散 = 30.25 + 30.25 + 6.25 + 2.25 + 20.25 + 56.256 = 145.56 = {{displaystyle {frac {30.25 + 30.25 + 6.25 + 2.25 + 20.25 + 56.25}{6}} = {{frac {145.5}{6}} = {}}となります．24.25

7. 7 式と関連付ける。このメソッドの冒頭の式とどう一致するかわからない場合は、問題の全体を手書きで書き出してみてください。平均値との差を求め、それを2乗すると、(x1{displaystyle x_{1}}-μ)2{displaystyle ^{2}}, (x2{displaystyle x_{2}}-μ)2{displaystyle ^{2}}の値が得られます。となり、 (xn{displaystyle x_{n}} - μ)2{displaystyle ^{2}} まで続く。ここで xn{displaystyle x_{n}} は集合の最後のデータ点である。これらの値の平均を求めるには、それらを足し合わせてnで割ります： ( (x1{displaystyle x_{1}} - μ)2{displaystyle ^{2}})+ (x2{displaystyle x_{2}} - μ)2{displaystyle ^{2}} + ...+ ...+ (xn{displaystyle x_{n}} - μ)2{displaystyle^{2}} + ...)/ n 分子をシグマ表記に書き換えると、(∑ (xi{displaystyle x_{i}} - μ)2{displaystyle ^{2}})/n という分散式が得られます。

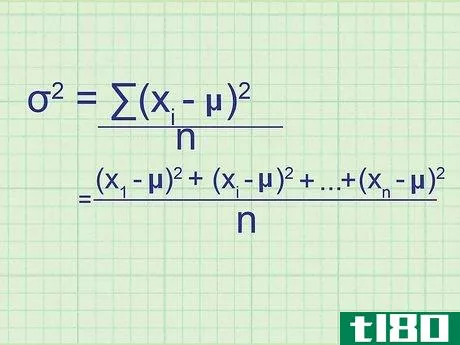
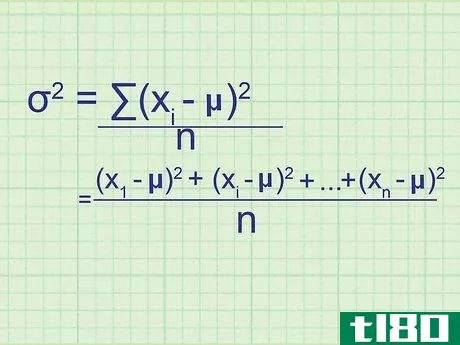
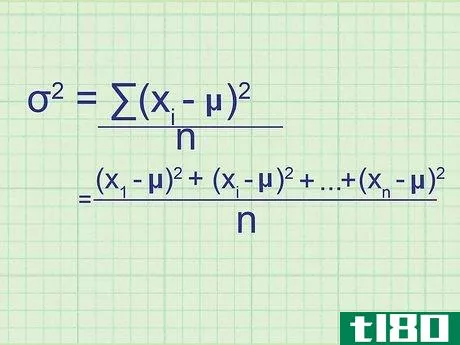
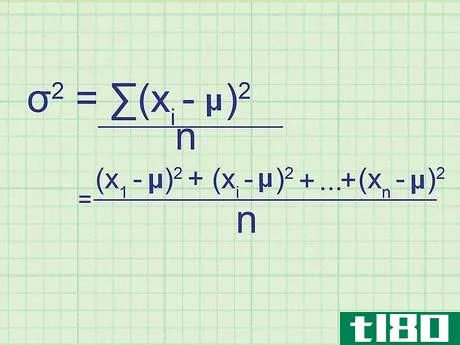
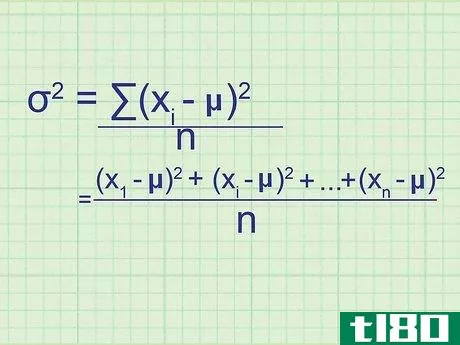
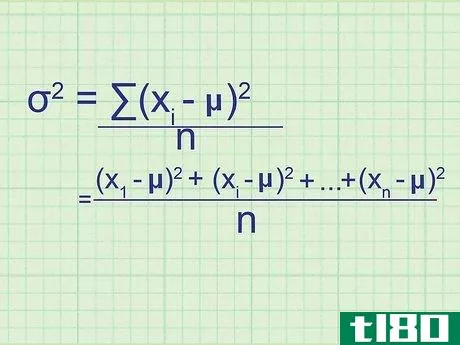
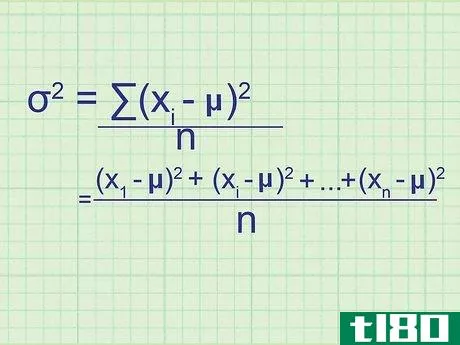
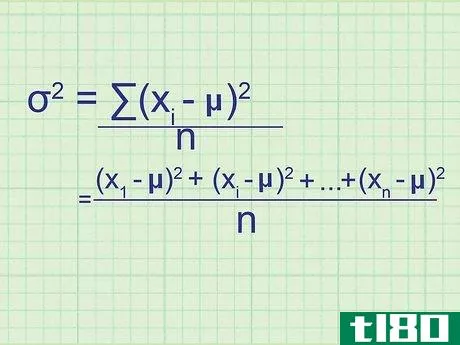
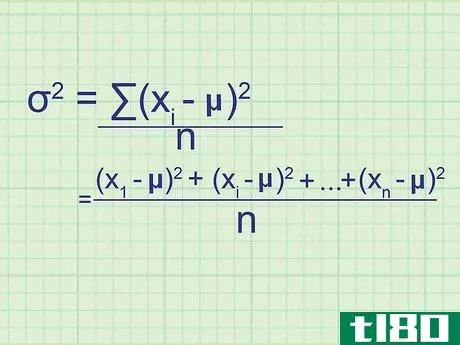
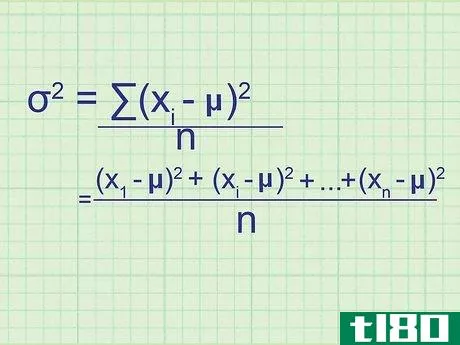
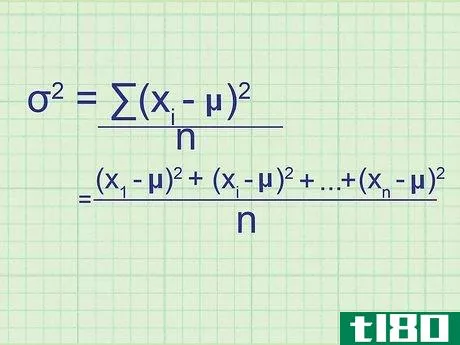
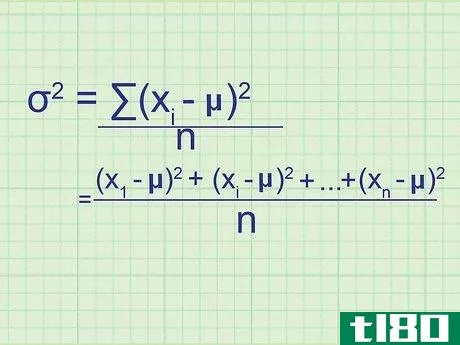
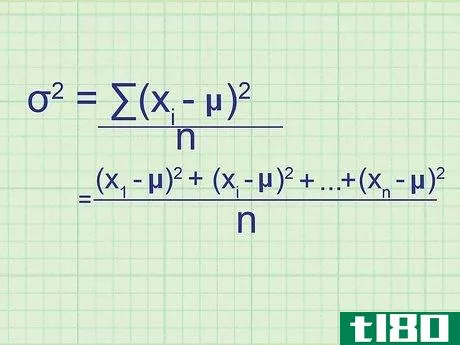
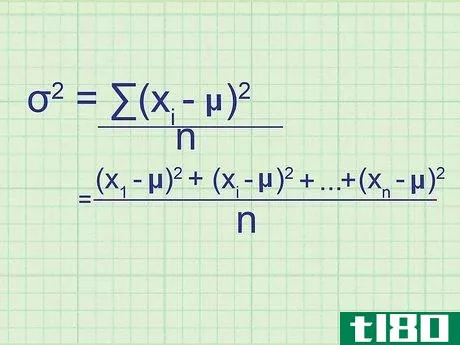
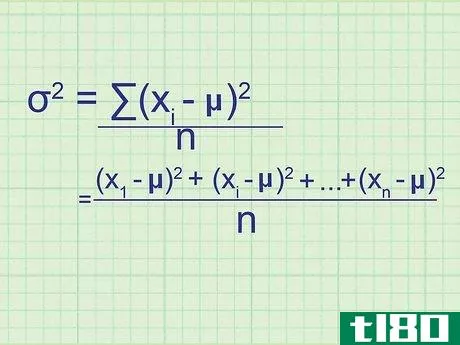
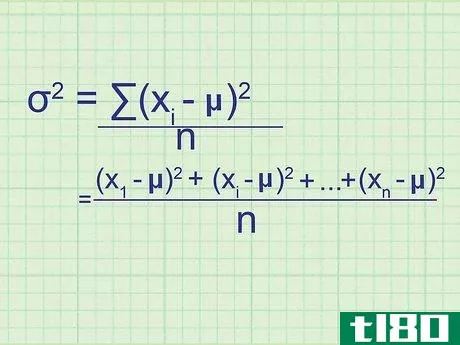
分散計算のヘルプ

差分チートシート

• 分散の解釈は難しいので、通常はこの値を起点に標準偏差を算出する。
• 試料を分析する際、分母に「n」ではなく「n-1」を使うのは、ベッセル補正と呼ばれる手法です。サンプルは母集団全体の推定値に過ぎず、サンプルの平均値はこの推定値に合うようにバイアスがかかっています。今回の補正では、このバイアスを除去しています。これは、n - 1個のデータ点をリストアップしたら、最後のn個目の点は、特定の値だけが分散の式で使われる標本平均（x_305）につながるので、すでに境界が決まっていることに関係しています。