如何解双摆(solve the double pendulum)

二摆是经典力学中对初始条件高度敏感的问题。控制双摆的运动方程可以用拉格朗日力学找到，尽管这些方程是耦合的非线性微分方程，只能用数值方法求解。...

台阶

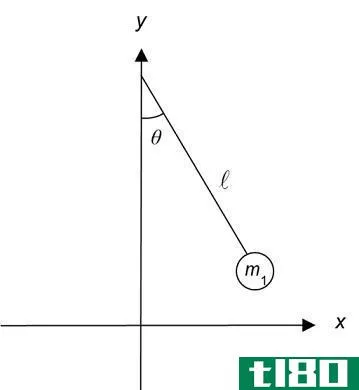
1.解决问题。我们可以想象一个长度为L1{\displaystyle L{1}和L2，{\displaystyle L{2}，}和质量为m1{\displaystyle m{1}和m2的双摆。{\displaystyle m_{2}.}第一个bob与垂直方向成角度θ1{\displaystyle\theta{1}}，第二个bob与垂直方向成角度θ2。{\displaystyle\theta{2}利用θ1{\displaystyle\theta{1}和θ2{\displaystyle\theta{2}作为这个问题的广义坐标是很方便的。本文的目的是推导双摆的拉格朗日方程，并使用欧拉-拉格朗日方程来获得运动方程。

$L_{{1}}$

$L_{{2}},$

$m_{{1}}$

$m_{{2}}.$

$\theta _{{1}}$

$\theta _{{2}}.$

$\theta _{{1}}$

$\theta _{{2}}$

2找到第一个鲍勃的能量。动能仅为K1=12m1L12θ˙12，{\displaystyle K{1}={\frac{1}{2}}m{1}L{1}{2}{\dot{theta}}{1}{2}，而势能是用三角学求出的。因为角度是相对于垂直方向的，所以我们需要余弦分量。因此，势能读数为U1=−m1gL1cos⁡θ1，{\displaystyle U{1}=-m{1}gL{1}\cos\theta{1}，其中g{\displaystyle g}是重力加速度。电势为负值，因为我们使用的是正y{\displaystyle y}轴向上的约定。
3.找出第二个鲍勃的能量。第二个bob更复杂，因为它的位置也取决于第一个bob。我们不能简单地用同样的方式写出它的动能，因为第二个鲍勃的位置也会随着第一个鲍勃而改变。因此，我们需要写出它的位置（x，y）{\displaystyle（x，y）}，然后进行微分以获得正确的速度。势能就是两个长度的余弦分量之和。U2=−m2g（L1cos）⁡θ1+L2cos⁡θ2{\displaystyle U{2}=-m{2}g\左（L{1}\cos\theta{1}+L{2}\cos\theta{2}\right}第二个bob的x{\displaystyle x}和y{\displaystyle y}位置如下所示。同样，我们使用三角学来挑选合适的分量。x=L1sin⁡θ1+L2sin⁡θ2{\displaystyle x=L_{1}\sin\theta{1}+L_{2}\sin\theta{2}}y=L1cos⁡θ1+L2cos⁡θ2{\displaystyle y=L_{1}\cos\theta{1}+L_{2}\cos\theta{2}现在我们根据时间来区分。注意，θ1=θ1（t）{\displaystyle\theta{1}=\theta{1}（t）}和θ2=θ2（t）{\displaystyle\theta{2}=\theta{2}（t）}都依赖于时间。x˙=L1cos⁡θ1θ˙1+L2cos⁡θ2θ˙2{\displaystyle{\dot{x}}=L{1}\cos\theta{1}{\dot{\theta}}1}+L{2}\cos\theta{2}{\dot{\theta}}}y}=−L1sin⁡θ1θ˙1−L2sin⁡2.0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1}{2}m \左（{dot{x}}^{2}+{dot{y}}^{2}\右），}我们需要将这些项平方。交叉项的引入是运动方程最终变得有些复杂的部分原因。x˙2=L12cos2⁡θ1θ˙12+L22cos2⁡θ2θ˙22+2llll2cos⁡θ1cos⁡3.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1}L{2}\cos\theta{1}\cos\theta{2}{\dot{\theta}}}{1}{\dot{\theta}}}}}y}2=L12sin2⁡θ1θ˙12+L22sin2⁡θ2θ˙22+2L1L2sin⁡θ1sin⁡3.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 5 5 5 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1}L{2}\sin\theta{1}\sin\theta{2}{\dot{\theta}}{1}{\dot{\theta}}}{2}在下面，我们使用身份cos⁡θ1cos⁡θ2+sin⁡θ1sin⁡θ2=cos⁡(θ2−θ1）{\displaystyle\cos\theta{1}\cos\theta{2}+\sin\theta{1}\sin\theta{2}=\cos（\theta{2}-\theta{1}）来简化表达式。K2=12m2（L12θ˙12+L22θ˙22+2lll2θ˙1θ˙2cos⁡(θ2−（1）1）3）3）1）3）3）3）1）3）1）3）1）1）3）1）1）1）3）1）1）1）1）1）3）3）3）3）3）1）1）3）3）1）3）3）1）1）3）3）3）3）3）1）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）1）3）3）1）1）3）1）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）3）））dot{\theta}}{2}\cos（\theta{2}-\theta{1}）\right）}
4写出系统的拉格朗日函数。拉格朗日函数就是动能减去势能L=K−U.{\displaystyle{\mathcal{L}}=K-U.}这相当混乱，尤其是因为交叉项。L=12m112θ˙12+12m2（L12θ˙12+L22θ˙22+2ll2θ˙1θ˙2cos⁡(θ2−θ1））+m1gL1cos⁡θ1+m2g（L1cos）⁡θ1+L2cos⁡θ2{\displaystyle{\begin{aligned}{\mathcal{L}}={\frac{1}{2}}m{1}L{1}{2}{\dot{\theta}}}{1}{2}&amp+{{1}{{1}{{1}{{1}{{1}{{1}{{{1}{{1}{{{1}{{{{1}{{{{{1}{{{{1}}{{{1}}{{{{1}}{{{1}}{{{1}{1}{{1}{{1}{{{{{1}}}}{{{{{{{1}}}}{{{{{{{1}}}}}{{{{{{{{{{1}}}}}}}{{{{{{{}}}}}}}}}}}}}}}}}{{{{{{{{{{{{{{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\cos（\theta{2}-\theta{1}）\right）\\&amp+m{1}gL{1}\cos\theta{1}+m{2}g\left（L{1}\cos\theta{1}+L{2}\cos\theta{2}\right）\end{aligned}
5使用欧拉-拉格朗日方程。欧拉-拉格朗日方程如下所示：∂L∂qi=滴滴涕∂L∂qi{729;，{\ displaystyle{\frac{\partial{\mathcal{L}}}{\partial q{i}}={\frac{\mathrm{d}}{\mathrm{d}}}{\mathrm{d}t}{\frac{\partial{\mathcal{L}}}}{\partial{dot{q{i}}}，其中qi\displaystyle{i}指的是广义坐标，在这种情况下。因此，我们必须采用导数。∂L∂θ1=m2L1L2θ˙1θ˙2sin⁡(θ2−θ1)−m1gL1sin⁡θ1−m2gL1sin⁡3.1{{\显示风格{{\显示风格{\ \显示风格{{\网页网页[[[[[1}}}{{{\网页[1}}}{{\网页[1}{{\网页[1}}{{\网页[1{\显示风格[1{\显示风格{\网页网页[[1}{\网页[[[[[1}}{\网页[[1}}{\网页[1}}}}}}}{{{{{{\网页[1}[1}[1}}}}}}}}}}}{{{{{{{{{1}......................................................................................_{2}gL_{1}\sin\theta_{1}∂L∂θ1˙=m1L12θ1˙+m2L12θ1˙+m2L1L2θ2˙cos⁡(θ2−3.1元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元\ dot{\theta{2}}\cos（\theta{2}-\theta{1}）∂L∂θ2=−m2L1L2θ1˙θ2˙sin⁡(θ2−θ1)−m2gL2sin⁡θ2{\displaystyle{\frac{\partial{\mathcal{L}}}}{\partial\theta{2}}}=-m\u{2}L\u{1}L\u{2}{\dot{\theta{1}}}}{\dot{\theta{2}}}}\sin{1}-m\u{2}gL\u{2}\sin\theta\u{2}}∂L∂θ2˙=m2L22θ2˙+m2L1L2θ1˙cos⁡(θ2−3.1元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元元-滴滴涕∂L∂θ1˙=+（m1+m2）L12θ1¨+m2L1L2θ2¨cos⁡(θ2−θ1)−m2L1L2θ2˙sin⁡(θ2−θ1)(θ2˙−θ1˙）{\displaystyle{\begin{aligned}{\frac{\mathrm{d}}{\mathrm{d}t}{\frac{\partial{\mathcal{L}}}{\partial{\dot{\theta{1}}}}=&amp+（m{1}+m{2}）L{1}{2}{\ddot{\theta{1}}+m{2}L{1}L{2}{\ddot{\theta{2}\cos（\theta{2}-\theta{1}）\&amp-m{2}L{1}L{2}{\dot{\theta{2}}}\sin（\theta{2}-\theta{1}）\left（{\dot{\theta{2}}}-{\dot{\theta{2}}-{\theta{1}\right）\end{aligned}ddt}∂L∂θ2˙=+m2L22θ2¨+m2L1L2θ1¨cos⁡(θ2−θ1)−m2L1L2θ1˙sin⁡(θ2−θ1)(θ2˙−θ1˙）{\displaystyle{\begin{aligned}{\frac{\mathrm{d}}{\mathrm{d}t}}{\frac{\partial{\mathcal{L}}}{\partial{\dot{\theta{2}}}}=&amp+m{2}L{2}{2}{\ddot{\theta{2}}+m{2}L{1}L{2}{\ddot{\theta{1}}\cos（\theta{2}-\theta{1}）\&amp-m{2}L{1}L{2}{\dot{\theta{1}}}\sin（\theta{2}-\theta{1}）\left（{\dot{\theta{2}}-\theta{2}}-{\dot{\theta{1}}\right）\end{aligned}
6.研究运动方程。经过一点简化，我们得到了这两个方程。不可能解析求解这些方程，但可以使用Mathematica、Matlab或类似软件进行数值求解。−（m1+m2）gL1sin⁡θ1=m2L1L2（θ2–cos）⁡(θ2−θ1)−θ˙22sin⁡(θ2−θ1）+（m1+m2）L12θ1¨−m2gL2sin⁡θ2=m2L1L2（θ1–cos）⁡(θ2−θ1）+θ˙12sin⁡(θ2−θ1）+m2L22θ2{\displaystyle{\begin{aligned}-（m{1}+m{2}）gL{1}\sin\theta{1}&amp={2}{{2}{2}{{2}{2}{2}{2}{{2}{{2}{{2}{{2}{{2}{{{2}{{{2}{{2}{{2}{2}{2}{1}{{1}{1}{{1}{{1}{1}{{1}{1}{{1}1}}{{1}{1}{{{{1}}{{1}1}{{{1}{{{{1}1}1}}{{{{{{1}}}}}{{{{{1}1}}}}}1}2}2}{{{2}{{{{{2}{{{{{{2}2}}}}theta{1}}\\\-m{2}gL{2}\sin\theta{2}&amp={2}{{2}{2}{{2}{2}{2}{2}{2}{{2}{2}{{2}{{2}{{2}{{2}{{2}{{2}{2}{2}{1}{1}{1}{1}{1}2}左（{\DD0\DDT T{{...........教学塔{{{{2}{{2}{2}{2}2}{{2}2}{2}2}2}2}2}2}{{2}2}{2}2}2}2}2}2}2}2}2}2}2}2}2}2}2}2}}}}\结束{aligned}}

发表于 2022-04-30 10:21
阅读 ( 35 )
分类：教育

你可能感兴趣的文章

如何同时消除excel中所有的数字符号（#）错误？

...驱动的问答网站分组。问题超级用户读者M.Hesse想知道如何同时消除Microsoft Excel中的所有数字符号（#）错误： When using Microsoft Excel, I usually solve ##### errors by double-clicking the offending column headers. This can become a bit tedious, however, when t...

发布于 2021-04-10 10:45
阅读 ( 172 )

从提示框：即时调整窗口大小，包含鼠标光标，了解电池配置

...周我们将介绍一个超级简单的调整窗口大小的快捷方式，如何在多监视器设置中包含鼠标，以及如何检查电池配置。单击一次即可垂直扩展窗口读者查尔斯在俄亥俄州撰文，分享了一个对我们来说全新的妙招： When you need to m...

发布于 2021-04-12 23:14
阅读 ( 170 )

如何用运动方程解运动问题(solve motion problems using equations of motion)

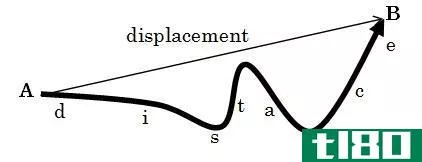
...题，可以使用四个“suvat”方程。我们将看看这些方程是如何推导出来的，以及如何用它们来解决沿直线运动的物体的简单运动问题。距离(distance)和取代(displacement)的区别 Distance is the total length of the path traveled by an object. This is a ...

发布于 2021-06-27 03:01
阅读 ( 259 )

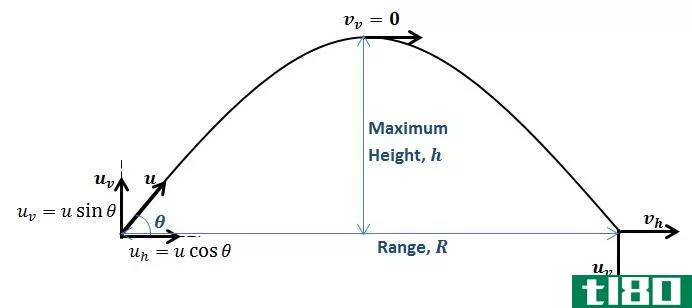
如何解决弹丸运动问题(solve projectile motion problems)

射弹是涉及二维的运动。为了解决弹丸运动问题，取两个相互垂直的方向（通常，我们使用“水平”和“垂直”方向），并将所有矢量（位移、速度、加速度）作为沿每个方向的分量。在弹丸中，垂直运动独立于水平运...

发布于 2021-06-27 03:02
阅读 ( 265 )

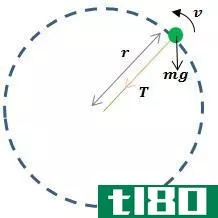
如何解决垂直圆周运动问题(solve vertical circular motion problems)

在本文中，我们将研究如何解决垂直圆周运动问题。解决这些问题的原理与解决向心加速度和向心力问题的原理相同。与水平圆不同的是，作用在垂直圆上的力随着它们的转动而变化。我们将考虑两种情况下物体在垂直...

发布于 2021-06-27 03:07
阅读 ( 418 )

如何解决动量问题(solve momentum problems)

在这里，我们将看看如何解决动量问题，在一维和二维使用守恒定律的线性动量。根据这个定律，只要没有外力作用，粒子系统的总动量就保持不变。因此，解决动量问题需要计算系统在相互作用前后的总动量，并将两...

发布于 2021-06-27 03:19
阅读 ( 339 )

单摆(simple pendulum)和复摆(compound pendulum)的区别

...别，所以这是一个相当定性的区别。什么是单摆(a simple pendulum)？如前所述，在单摆中，悬挂物体的尺寸明显小于物体重心到悬挂轴的距离。这使得我们可以把质量看成是一个点。我们还假设悬挂在物体上的“弦”是无弹性和无...

发布于 2021-06-27 04:15
阅读 ( 676 )

“爷爷的魔方”-常见应用论文样本，选项4

...，他把自己描述成一个不擅长解决谜题或弄明白家用物品如何工作的人。这种谦逊和诚实的态度揭示了一种成熟的水平，这种成熟可以在一篇申请论文中非常好地发挥作用。话虽如此，这篇文章确实透露出一种平静的决心，因...

发布于 2021-09-08 03:38
阅读 ( 210 )

如何使用关键字final防止java中的继承(prevent inheritance in java using the keyword final)

...：有关使用此Account和OverdraftAccount类的其他讨论，请参见如何将子类视为超类）。让我们为每个Account和OverdraftAccount类创建一个实例： Account bobsAccount = new Account(10); bobsAccount.depositMoney(50); OverdraftAccount jimsAccount = new Overdraf...

发布于 2021-09-24 00:33
阅读 ( 183 )

如何逐步解决代数问题(solve algebra problems step-by-step)

...下面列出了解决代数问题的5个步骤，下面将帮助您学习如何首先确定问题。找出问题所在。确定你所知道的。制定一个计划。执行计划。验证答案是否有意义。找出问题所在远离计算器；先动动脑筋。你的头脑在迷宫...

发布于 2021-10-10 22:51
阅读 ( 246 )

如何解双摆(solve the double pendulum)

台阶

你可能感兴趣的文章

相关推荐