如何计算散度和旋度(calculate divergence and curl)
第1部分第1部分,共2部分:分歧
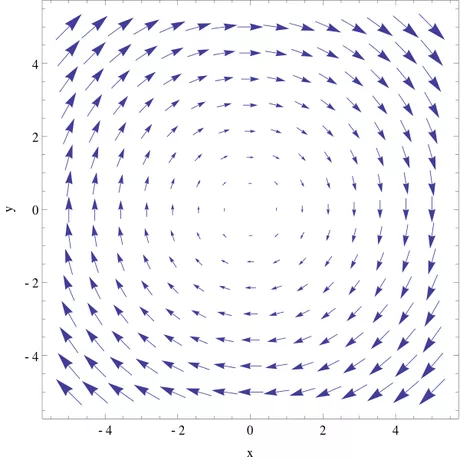
- 1了解分歧是什么。散度是对特定点的源或汇的度量换句话说,多少是流入或流出一个点。因此,它仅为向量场定义,并输出标量。下面是一个正散度场的例子。分歧由div{\displaystyle\operatorname{div}}或∇⋅{\displaystyle\nabla\cdot},其中点表示获取点积的相似性。
- 2将偏导数与F{\displaystyle\mathbf{F}分量的点积相加。这适用于仅在笛卡尔坐标系中定义的向量场F=Fxx^+Fyy^+Fzz^{\displaystyle\mathbf{F}=F_{x}\mathbf{\hat{x}}+F_{y}\mathbf{\hat{y}+F_{z}\mathbf{\hat{z}}。∇⋅F=(∂∂十、∂∂Y∂∂z)⋅(外汇、财年、Fz)=∂外汇∂x+∂Fy∂y+∂Fz∂“左({\FRC{{\部分{{{\部分}{{{\部分}{\部分x}}},,{{\FRC{{\部分{{\部分{{{\部分y}}},,{\\\显示风格\Na布拉\cdot\cdot\METOT\MEBOT\Na布拉\Na布拉\Na布拉\CDT\MET\MET\门门门邦邦邦邦邦邦邦邦邦邦邦邦[[[[[[F}}{{{{{{{{{{{{{{{{{{{{{{{{{....................................缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸...概概概概概概概,,,,,,{{{{{{{{{{,,,,{{{{z}{\部分z}}
- 3参考以下公式。如果向量场F{\displaystyle\mathbf{F}}是以柱坐标(ρ,ν,z){\displaystyle(\rho,φ,z)}或球坐标(r,θ,φ){\displaystyle(r,θ,θ,φ)}(其中θ{\displaystyle\θ是极角)给出的,则散度没有简单的形式。∂外汇∂x+∂Fy∂y+∂Fz∂z{\displaystyle{\frac{\partial F_{x}}{\partial x}}+{\frac{\partial F_{y}}{\partial y y}}+{\frac{\partial F_{z}}{\partial z}}}1ρ∂(ρFρ)∂ρ+1ρ∂Fñ∂ϕ+∂Fz∂z{\displaystyle{\frac{1}{\rho}}{\frac{\partial(\rho F{\rho}}}}{\partial\rho}}+{\frac{1}{\rho}}{\frac{\partial F{\phi}}{\partial\phi}+\frac{\partial F{phi z}}}{∂(r2Fr)∂r+1rsinθ∂∂θ(Fθsin)θ) +1rsinθ∂Fñ∂{{7{{{{{{{{{{{{{{{{{{{{{}}}{{{{}{{{{{{{{{{{{{{{{{{{{}}}}{{{{{{{{{{{{{{{{{{{{{{}}}{{{{{{{{{}}}}}}{{{{{{{{{{}}}}}}}}}}}{{{{{{{{{{{{{{{{{{{{{}}}}}}}}}}}}{{{{{{{{{{{{{}}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{}}}}}}}}}}}部分部分(r}}}}{{{{{{{{{{{{{{}}}}}}}}}}}}}}
- 4计算下列函数的散度。F=(3x2)−5x2y4)x^+(xy4z2−罪(2x2z3)y^+(5z2+yz)z^{\displaystyle\mathbf{F}=(3x^{2}-5x^{2}-y^{4})\mathbf{hat{x}}+(xy^{4}z^{2}-\sin 2x^{2}-z^{3}\mathbf{hat}{y}∇⋅F=6x−10xy4+4xy3z2+y+10z{\displaystyle\nabla\cdot\mathbf{F}=6x-10xy{4}+4xy{3}z^{2}+y+10z}正如你们所看到的,我们已经从一个向量场映射到了一个标量场。
第2部分第2部分,共2部分:卷曲
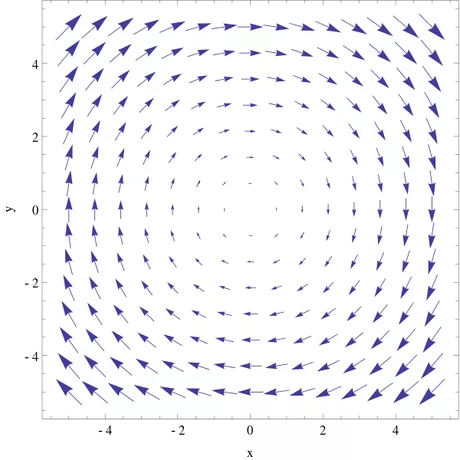
- 1了解什么是卷曲。旋度是为向量场定义的,直观地说,是任意点的循环量。操作符输出另一个向量场。现实生活中的漩涡是由水组成的,就像一个具有非零旋度的向量场。上面是一个负旋度场的例子(因为它是顺时针旋转的)。curl由curl{\displaystyle\operatorname{curl}}或∇×{\displaystyle\nabla\times},其中times符号表示采用叉积的相似性。
- 2.设置行列式。函数的旋度类似于两个向量的叉积,因此旋度算子用a表示∇×.{\displaystyle\nabla\times.}和以前一样,只有在笛卡尔坐标系中定义了F{\displaystyle\mathbf{F}时,这种助记符才有效。∇x F=|x^y^z^∂/∂十、∂/∂Y∂/∂zFxFyFz |{\displaystyle\nabla\times\mathbf{F}={\begin{vmatrix}\mathbf{\hat{x}}&;\mathbf{\hat{y}}&;\mathbf{\hat{z}\\\\partial/\partial x&;\部分/\部分y&;\部分/\partial z\\F_{x}&;F_{y}&;F_{z}\end{vmatrix}
- 3.找出矩阵的行列式。下面,我们通过辅因子展开(通过未成年人展开)来实现。∇×F=(∂Fz∂Y−∂Fy∂z) x^−(∂Fz∂十、−∂外汇∂z) y^+(∂Fy∂十、−∂外汇∂y) 3.0{{{7}}{{{\\显示风格\Na布拉\ \时间\ \泰国布布布利亚\ \10 10 10 10{{{{{{}}}{{{{{{{{{}}}{{{{{\\布布布布利亚\儿童儿童儿童[[[[3\布布布布布布利亚\ \儿童儿童儿童[[[[3}}}}}{{{{{{{}}}}}}}}{{{{{\部分y}}}}}}}}}{{{{{{{{{{{\部分y}}}}}}}}}}}}{{{{{{{{\缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸}}}}}}}}{{{{{{{{{{{缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸缅甸}}}}}}}}}}}}}}}}}}}}}}{{{{{F{y}{\partial x}}-{\frac{\partial F{x}}{\partial y}}}\right)\mathbf{\hat{z}}
- 4参考以下公式。如果F{\displaystyle\mathbf{F}}在柱坐标或球坐标中,旋度没有简单的形式。(∂Fz∂Y−∂Fy∂z) x^−(∂Fz∂十、−∂外汇∂z) y^+(∂Fy∂十、−∂外汇∂y) 7.7{{{{{{{{{{{{{{{{{{{{{{}}}}}{{{{{{{{{{{{{}}}{{{{{{{{}}}{{{{{}}}}}{{{{}}}}}}{{{{{{{{{{}}}}}{{{{{}}}}}}}{{{{{{{{}}}}}}}}}}}}}{{{{{{{{{{}}}}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{{}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{{{{{{{{{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}x}-{\frac{\partial F{x}}{\partial y}}\right\mathbf{\hat{z}}}(1ρ∂Fz∂ϕ−∂Fñ∂z) ρ^−(∂Fz∂ρ−∂Fρ∂z) ñ^+1ρ(∂(ρFñ)∂ρ−∂Fρ∂7.7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 5 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 hat{\phi}}+{\frac{1}{\rho}}\left({\frac{\partial(\rho F_{\phi})}{\partial\rho}}-{\frac{\partial F_{\rho}{\partial\phi}}\right)\mathbf{\hat{z}}}1rsinθ(∂∂θ(Fñsin)θ)−∂Fθ∂ν)r^−1r(∂∂r(射频)−1英寸θ∂Fr∂ν)θ^+1r(∂∂r(rFθ)−∂Fr∂θ) ñ^{\displaystyle{\begin{aligned}{\frac{1}{r\sin\theta}}\left({\frac{\partial}{\partial\theta}}(F{\phi}\sin\theta){\frac{\partial F{\theta}{\partial\phi}\right)\mathbf{\hat{r}&-{\frac{1}{r}}\左({\frac{\partial}{\partial r}}}(rF{\phi}){\frac{1}{\sin\theta}}{\frac{\partial F{r}{\partial\phi}\右){\boldsymbol{\hat{\theta}\\\\&+{\frac{1}{r}}左({\frac{\partial}{\partial r}}}(rF{\theta}){\frac{\partial F{r}}}右{\partial\theta}右{\boldsymbol{\hat{\phi}}\end{aligned}
- 5计算以下函数的旋度。F=(5x2y2)−7xz3)x^+(4x−5xy−y4)y^+(xz+z2)z^{\displaystyle\mathbf{F}=(5x^{2}-7xz{3})\mathbf{\hat{x}+(4x-5xy-y^{4})\mathbf{\hat{y}+(xz+z^{2})\mathbf
- 6设置行列式。∇x F=|x^y^z^∂/∂十、∂/∂Y∂/∂zFxFyFz |{\displaystyle\nabla\times\mathbf{F}={\begin{vmatrix}\mathbf{\hat{x}}&;\mathbf{\hat{y}}&;\mathbf{\hat{z}\\\\partial/\partial x&;\部分/\部分y&;\部分/\partial z\\F_{x}&;F_{y}&;F_{z}\end{vmatrix}}Fx=5x2y2−7xz3{\displaystyle F_{x}=5x^{2}y^{2}-7xz^{3}Fy=4x−5xy−y4{\displaystyle F{y}=4x-5xy-y^{4}}Fz=xz+z2{\displaystyle F{z}=xz+z^{2}
- 7计算行列式。(∂Fz∂Y−∂Fy∂z) x^=0−0{\displaystyle\left({\frac{\partial F_{z}}{\partial y}}-{\frac{\partial F_{y}}}{\partial z}}\right)\mathbf{\hat{x}}=0-0}(∂Fz∂十、−∂外汇∂z) y^=z−(−21xz2){\displaystyle\left({\frac{\partial F_{z}}{\partial x}}-{\frac{\partial F_{x}}}}{\partial z}\right)\mathbf{\hat{y}=z-(-21xz^{2})(∂Fy∂十、−∂外汇∂y) z^=(4)−5y)−10x2y{\displaystyle\left({\frac{\partial F{y}}{\partial x}}-{\frac{\partial F{x}}}{\partial y y}}\right)\mathbf{\hat{z}=(4-5y)-10x^{2}{y}
- 8.得出答案。∇×F=−(z+21xz2)y^+(4)−5y−10x2y)z^{\displaystyle\nabla\times\mathbf{F}=-(z+21xz^{2})\mathbf{\hat{y}+(4-5y-10x^{2}y)\mathbf{\hat{z}}注意,我们已经映射到另一个向量场。
- 有几个身份是有用的,值得记住。下面是更重要的二阶导数的部分列表。你可以通过直接计算来证明它们。∇⋅(∇×F)=0{\displaystyle\nabla\cdot(\nabla\times\mathbf{F})=0}∇×(∇f) =0{\displaystyle\nabla\times(\nabla f)=0}
- 拉普拉斯算子是一种复合算子,定义为梯度的散度∇⋅∇=∇2.{\displaystyle\nabla\cdot\nabla=\nabla^{2}我们用笛卡尔坐标写出拉普拉斯函数。这个算符在物理和工程中特别有用。例如,静电场的电势可以用泊松方程来描述,其中涉及拉普拉斯方程。∇2ϕ=∂2ϕ∂x2+∂2ϕ∂y2+∂2ϕ∂z2{\displaystyle\nabla^{2}\phi={\frac{\partial^{2}\phi}{\partial x^{2}}}+{\frac{\partial^{2}\phi}{\partial y^{2}}}+{\frac{\partial^{2}\phi
- 发表于 2022-05-18 07:55
- 阅读 ( 30 )
- 分类:教育
你可能感兴趣的文章
如何使用命令行查找计算机的地理位置?
...算机的位置,但是如果您决定使用命令行查找信息,您该如何进行呢?今天的超级用户问答有一些有用的建议,可以帮助读者找到他想要的信息。 今天的问答环节是由SuperUser提供的,SuperUser是Stack Exchange的一个分支,是一个由社...
- 发布于 2021-04-09 17:03
- 阅读 ( 162 )
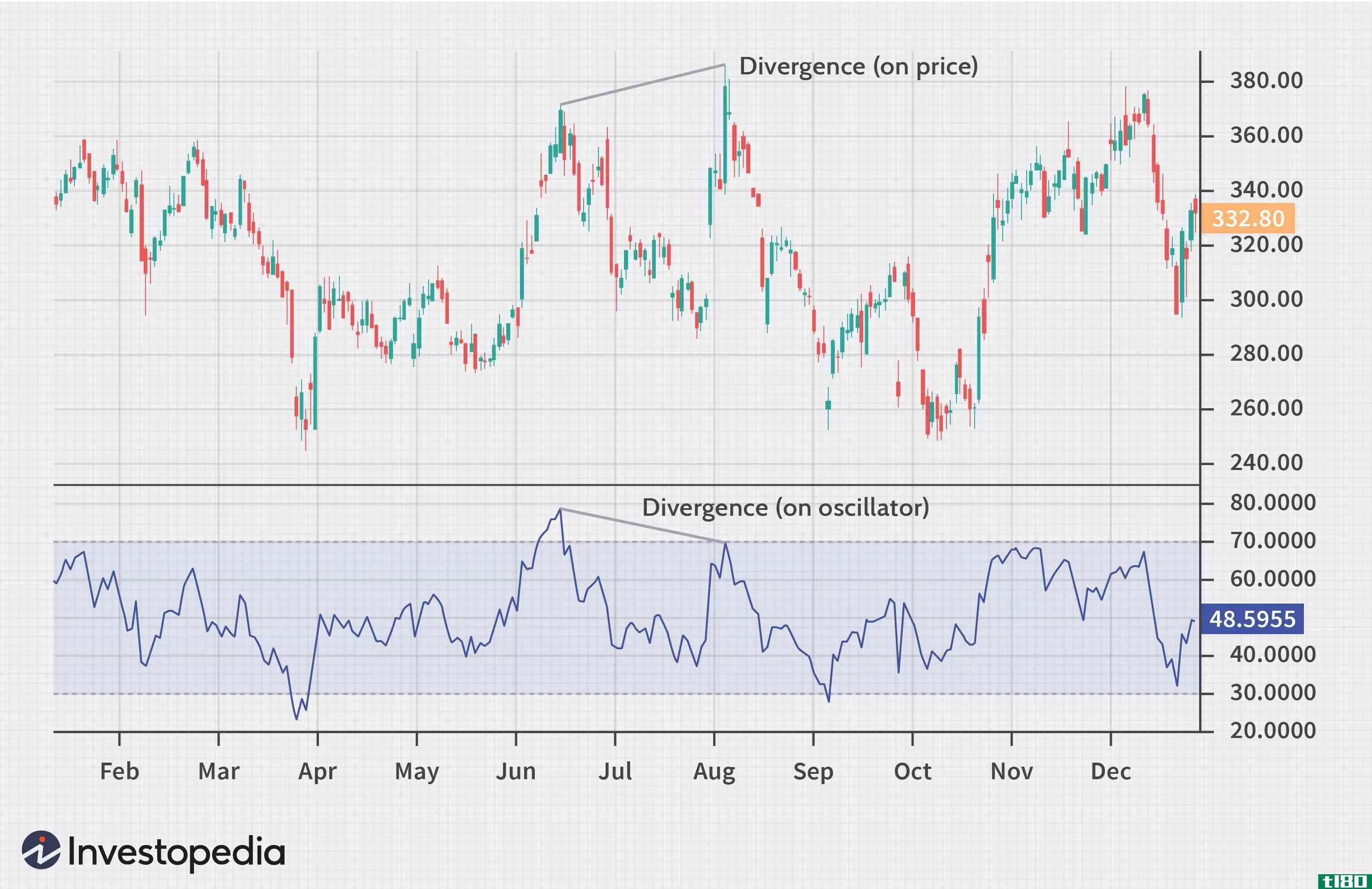
分歧的定义和使用
...所有主要的价格反转都存在,它只存在于一些市场。 散度告诉你什么 技术分析的分歧可能预示着一个重大的积极或消极的价格走势。当一项资产的价格创出新低,而货币流量等指标开始攀升时,就会出现正偏离。相反,负...
- 发布于 2021-06-01 15:15
- 阅读 ( 127 )
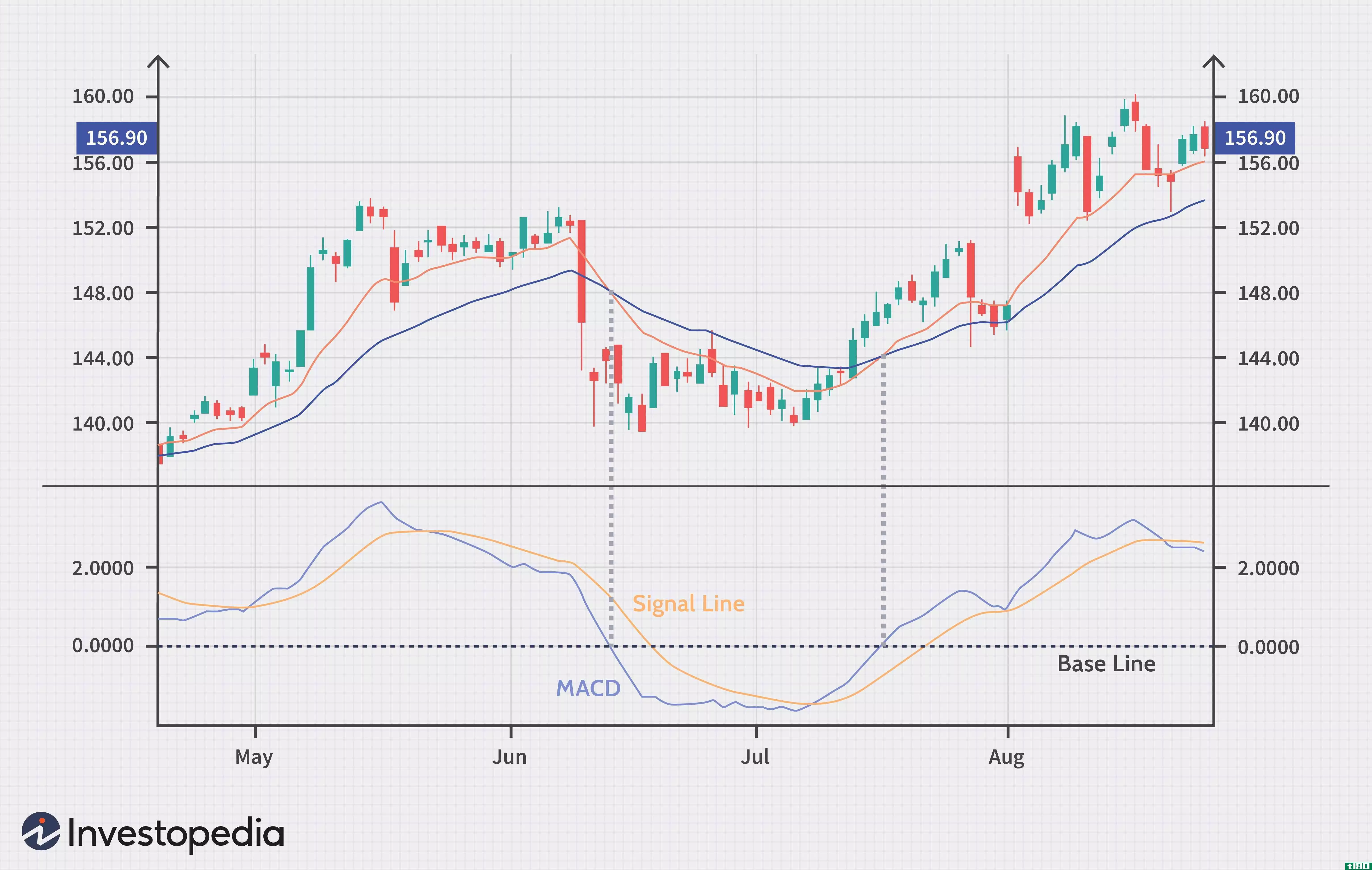
移动平均收敛-发散(macd)
...增长。 在下图中,您可以看到应用于价格图的两个均线如何对应于价格图下方指标中高于或低于基准线(虚线)的MACD(蓝色)交叉点。 MACD通常用直方图(见下表)显示,直方图显示MACD与其信号线之间的距离。如果MACD高...
- 发布于 2021-06-06 08:45
- 阅读 ( 215 )
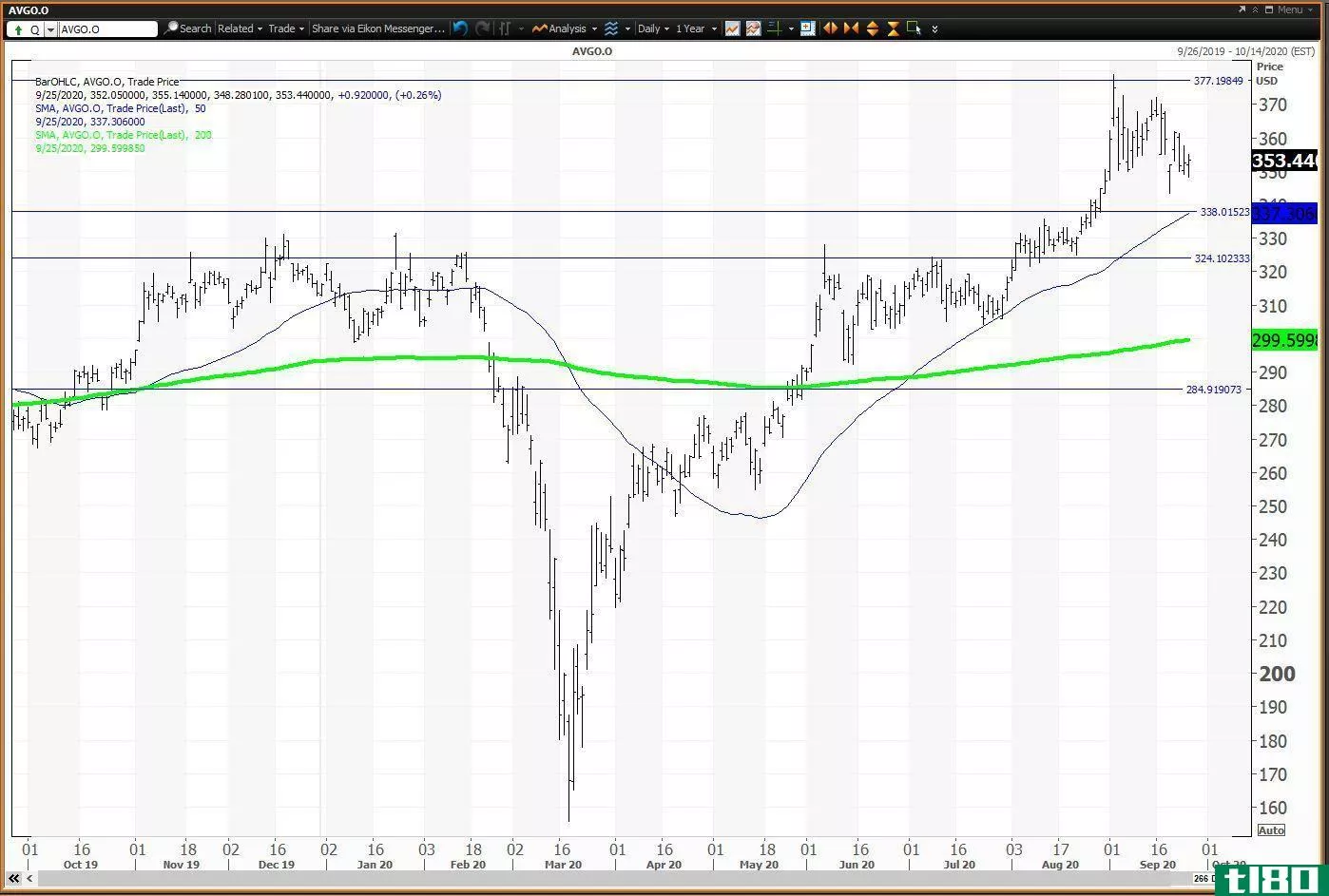
动量股broadcom(avgo)可能已见顶
...度报324.02美元。强势减持至半年度风险水平77.65美元。 如何使用我的价值水平和风险水平:该股2019年12月31日的收盘价是我专有分析的输入。半年度和年度水平仍在图表上。每次计算都使用这些时间范围内的最后九个结束点。 ...
- 发布于 2021-06-17 20:02
- 阅读 ( 133 )
分散(dispersion)和偏斜(skewness)的区别
...况的一种方法,这意味着它指定了数据集中的值在大小上如何不同。它是围绕中心点分布的统计分布的范围。它主要决定数据集围绕其中心点的项目的可变性。简单地说,它衡量的是平均值周围的变化程度。离散度的度量对于确...
- 发布于 2021-06-25 15:08
- 阅读 ( 551 )
如何计算坠落物体的空气阻力(calculate air resistance of a falling object)
...g downwards, and so there will be an upward resistive force on the paper. 如何计算物体在空中缓慢下落时的空气阻力 For objects which move slowly relative to the air (such as falling dust particles), the resistive force is directly proportional to the object’s velocity relative...
- 发布于 2021-06-27 02:57
- 阅读 ( 206 )
如何计算位移(calculate displacement)
...之前,让我们先定义位移,然后学习什么是位置向量以及如何编写它。 位移的定义 位移是对粒子初始位置和最终位置之间差异的测量。它是运动学中使用的基本量之一,也用于导出速度和加速度。位移是一个向量量,它有一个...
- 发布于 2021-06-27 02:58
- 阅读 ( 292 )
如何计算向心力(calculate centripetal force)
在学习如何计算向心力之前,让我们先看看什么是向心力,它是如何导出的。在圆形路径中移动的物体即使保持恒定速度也在加速。这种物体所经历的加速度称为向心加速度,它总是指向圆轨迹的中心。根据牛顿第二定...
- 发布于 2021-06-27 03:05
- 阅读 ( 198 )
如何计算已完成工时(calculate work done)
...功的能力,做功传递能量。测量能量的单位也是焦耳。 如何计算已完成工时-示例 例1 在一个操场上,一个坐在玩具车里的孩子被她的朋友向前拉,她的朋友用60牛顿的力沿着玩具车上的绳子拉着玩具车。绳子与地面成35度角。计...
- 发布于 2021-06-27 03:19
- 阅读 ( 140 )
如何计算动能(calculate kinetic energy)
在本文中,我们将研究如何计算动能。动能是物体运动所产生的能量,它取决于物体的速度和质量。物体的运动方向对动能没有影响。对于一个运动的物体,动能被定义为使物体从静止加速到它的速度所需要做的净功。...
- 发布于 2021-06-27 03:20
- 阅读 ( 119 )