如何求解微分方程(solve differential equations)
第1部分第1部分(共2部分):一阶方程
- 1线性一阶方程。在本节中,我们讨论了求解线性一阶微分方程的方法,包括在一般情况下以及在某些项设置为0的特殊情况下。我们假设y=y(x),{\displaystyle y=y(x),}p(x),{\displaystyle p(x),}和q(x){\displaystyle q(x)}是x.{\displaystyle x.}dydx+p(x)y=q(x){\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}+p(x)y=q(x}p(x)=0的函数。{\displaystyle p(x)=0。}根据微积分基本定理,函数导数的积分就是函数本身。然后我们可以简单地积分得到我们的答案。记住,计算不定积分会引入任意常数。y(x)=∫q(x)dx{\displaystyle y(x)=\int q(x)\mathrm{d}x}q(x)=0。{\displaystyle q(x)=0。}我们使用分离变量的技术。变量分离直观地将每个变量置于方程的不同侧面。例如,我们将所有y{\displaystyle y}项移到一边,将x{\displaystyle x}项移到另一边。我们可以将导数中的dx{\displaystyle\mathrm{d}x}和dy{\displaystyle\mathrm{d}y}视为可以移动的量,但请记住,这只是利用链式规则进行操作的简写。这些被称为微分的对象的确切性质超出了本文的范围。首先,我们得到方程两侧的每个变量。1岁=−p(x)dx{\displaystyle{\frac{1}{y}}\mathrm{d}y=-p(x)\mathrm{d}x}积分两侧。积分在两侧引入了一个任意常数,但我们可以在右侧合并它们。自然对数y=∫−p(x)dx{\displaystyle\ln y=\int-p(x)\mathrm{d}x}y(x)=e−∫p(x)dx{\displaystyley y(x)=e ^{-\int p(x)\mathrm{d}x}}}示例1.1。在最后一步中,我们利用指数定律ea+b=eaeb{\displaystyle e^{a+b}=e^{a}e^{b}},并将eC{\displaystyle e^{C}}替换为C{\displaystyle C},因为它同样是一个任意常数。dydx公司−2赖氨酸x={\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}2y\sin x=0}12ydy=sinxdx12lny=−余弦x+Clny=−2cosx+Cy(x)=Ce−2cosx{\displaystyle{\begin{aligned}{\frac{1}{2y}}\mathrm{d}y&=\sin x\mathrm{d}x\{\frac{1}{2}}\ln y&=-\cos x+C\\ n y&=-2\cos x+C\\y(x)&=Ce ^{-2\cos x}\end{aligned}}}p(x)≠0,q(x)≠0.{\displaystyle p(x)\neq 0\q(x)\neq 0}为了解决一般情况,我们引入了积分因子μ(x),{\displaystyle\mu(x),}一个x{\displaystyle x}的函数,通过将左侧置于公共导数下,使方程更容易求解。将两侧乘以μ(x)。{\displaystyle\mu(x)}μdydx+μpy=μq{\displaystyle\mu{\frac{\mathrm{d}y}{\mathrm{d}x}}+\mu py=\mu q}为了使左侧服从公共导数,我们必须具有以下条件。ddx(μy)=dμdxy+μdydx=μdydx+μpy{\displaystyle{\frac{\mathrm{d}}}{\mathrm{d}x}(\mu y)={\frac{\mathrm{d}\mu}{\mathrm{d}x}}y+\mu mu{\frac{\mathrm{d}y}{\mathrm{d}x}+\mu-py}后一个方程意味着dμdx=μp,{\displaystyle{\frac{\mathrm{d}\mu}{\mathrm{d}x}=\mu p,}具有以下解。这是求解每个线性一阶方程的积分因子。我们现在可以继续推导一个公式,用μ{\displaystyle\mu}来求解这个方程,但简单地进行计算更有指导意义。μ(x)=e∫p(x)dx{\displaystyle\mu(x)=e ^{\int p(x)\mathrm{d}x}}示例1.2。这个例子还引入了在给定初始条件下寻找微分方程特定解的概念。tdydt+2y=t2,y(2)=3{\displaytyle t{\frac{\mathrm{d}y}{\mathrm{d}t}+2y=t^{2},quad y(2)=3}dydt+2ty=t{\displaytyle{\frac{\mathrm{d}y}{\mathrm{d}t}+{\frac{2}{t}y=t}μ(t)=e∫p(t)dt=e2lnt=t2{\displaystyle\mu(t)=e{\int p(t)\mathrm{d}t}=e{2\ln t}=t{2}}ddt(t2y)=t3t2y=14t4+Cy(t)=14t2+Ct2{\displaystyle{\begin{aligned}{\frac{\mathrm{d}}}}{\mathrm{d}t}(t{2}y)&=t ^{3}\\t ^{2}y&={\frac{1}{4}}t^{4}+C\\y(t)&={frac{1}{4}}t{2}+{frac{C}{t{2}}}\end{aligned}}}3=y(2)=1+C4,C=8{displaystyle 3=y(2)=1+{frac{C}{4}},四元C=8}y(t)=14t2+8t2{displaystyle y(t)={frac{1}。{4}}t ^{2}+{\frac{8}{t ^{2}}}
- 2非线性一阶方程。在本节中,我们讨论求解某些非线性一阶微分方程的方法。没有封闭形式的通解,但某些方程可以使用以下技术求解。dydx=f(x,y){\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}}=f(x,y)}dydx=h(x)g(y)。{\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}=h(x)g(y)。}如果函数f(x,y)=h(x)g(y){f(x,y)=h(x)g(y)}可以分为每个变量的函数,则称方程是可分的。然后,我们继续使用与之前相同的方法。∫dyh(y)=∫g(x)dx{\displaystyle\int{\frac{\mathrm{d}y}{h(y}}}}=\int g(x)\mathrm{d}x}示例1.3。dydx=x3y(1+x4){\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}}={\frac{x^{3}}}{y(1+x^{4}}}}}}∫ydy公司=∫x31+x4dx12y2=14ln(1+x4)+Cy(x)=12ln(1+x4)+C{\displaystyle{\begin{aligned}\int y\mathrm{d}y&=\int{\frac{x ^{3}}{1+x ^{4}}}\mathrm{d}x\{\frac{1}{2}}}y ^{2}&={\frac{1}{4}}\ln(1+x ^{4})+C\\y(x)&={\frac{1}{2}}\ln(1+x ^{4})+C\end{aligned}}}dydx=g(x,y)h(x,y)。{\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}}={\frac{g(x,y)}{h(x,y)}}设g(x,y){\displaystyle g(x,y)}和h(x,y){\displaystyle h(x,y)}是x{\displaystyle x}和y的函数。{\displaystyle y。}则齐次微分方程是一个方程,其中g{\displaystyle g}和h{\displaystyle h}是相同阶的齐次函数。也就是说,该函数满足性质g(αx,αy)=αkg(x,y),{\displaystyle g(\alpha x,alpha y)=\alpha ^{k}g(x,y),}其中k{\displaystyle k}称为同质度。每个齐次微分方程都可以通过变量的充分变化转换为可分离方程,变量可以是v=y/x{\displaystyle v=y/x}或v=x/y。{\displaystyle v=x/y}示例1.4。上述关于同质性的讨论可能有些神秘。让我们通过一个例子来看看这是如何应用的。dydx=y3−x3y2x{\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}={\frac{y^{3}-x^{3}}{y^{2}x}}}}我们首先观察到这是y中的非线性方程。{\displaystyle y}我们还看到这个方程不能分离。然而,它是一个齐次微分方程,因为顶部和底部都是3次齐次的。因此,我们可以改变变量v=y/x.{\displaystyle v=y/x.}dydx=yx−x2y2=v−1v2{\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}={\frac{y}{x}}-{\frac{x^{2}}}{y^{2}}}=v-{\frac{1}{v^{2}}}}y=vx,dydx=DVDX+v{displaystyle y=vx,\quad{\frac{\mathrm{d}y}{\mathrm{d}x}}={\frac{\mathrm{d}v}{\mathrm{d}x}x+v}dvdxx=−1v2.{\displaystyle{\frac{\mathrm{d}v}{\mathrm{d}x}}x=-{\frac{1}{v ^{2}}}}}这现在是v.{\displaystyle v.}v(x)中的一个可分离方程=−3磅x+C3{\displaystyle v(x)={\sqrt[{3}]{-3\ln x+C}}}}y(x)=x−3磅x+C3{\displaystyle y(x)=x{\sqrt[{3}]{-3\ln x+C}}}}}dydx=p(x)y+q(x)yn。{\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}}=p(x)y+q(x)y ^{n}这是伯努利微分方程,一个非线性一阶方程的特例,其解可以用初等函数表示。乘以(1)−n) y−n、 {\displaystyle(1-n)y ^{-n}.}(1−n) y−ndydx=p(x)(1)−n) y1−n+(1−n) q(x){\displaystyle(1-n)y ^{-n}{\frac{\mathrm{d}y}{\mathrm{d}x}=p(x)(1-n)y ^{1-n}+(1-n)q(x}使用左侧的链式规则将方程转换为y1中的线性方程−n、 {\displaystyle y ^{1-n},},然后可以使用前面的技术求解。dy1型−ndx=p(x)(1)−n) y1−n+(1−n) q(x){\displaystyle{\frac{\mathrm{d}y ^{1-n}}}{\mathrm{d}x}}=p(x)(1-n)y ^{1-n}+(1-n)q(x}M(x,y)+n(x,y)dydx=0。{\displaystyle M(x,y)+N(x,y){\frac{\mathrm{d}y}{\mathrm{d}x}}=0这里,我们讨论精确方程。我们希望找到一个称为势函数的函数φ(x,y),{\displaystyle\varphi(x,y),},使得dφdx=0。{\displaystyle{\frac{\mathrm{d}\varphi}{\mathrm{d}x}}=0。}为了满足这个条件,我们有以下总导数。总导数允许额外的变量依赖性。为了计算φ{\displaystyle\varphi}相对于x的总导数,{\displaystyle x,},我们考虑了y{\displaystyle y}也可能依赖于x.{\displaystyle x.}dφdx的可能性=∂φ∂x+∂φ∂ydydx{\displaystyle{\frac{\mathrm{d}\varphi}{\mathrm{d}x}}={\frac{\partial\varphi}{\partial x}+{\frac{\partial\varphi}{\partial y}}{\frac{\mathrm{d}y}{\mathrm{d}x}}}比较项,我们有M(x,y)=∂φ∂x{\displaystyle M(x,y)={\frac{\partial\varphi}{\partial x}}}}和N(x,y)=∂φ∂y、 {\displaystyle N(x,y)={\frac{\partial\varphi}{\partial y}}光滑函数的混合导数彼此相等是多变量微积分的标准结果。这有时被称为克莱罗定理。如果以下条件成立,则微分方程是精确的。∂M∂y=∂N∂x{\displaystyle{\frac{\partial M}{\partial y}}={\frac{\partial N}{\partial x}}}求解精确方程的方法类似于寻找pote
- 许多微分方程根本无法用上述方法求解,尤其是讨论部分提到的方法。当方程包含可变系数且不是Euler-Cauchy方程时,或当方程是非线性时,会发生这种情况,除非有一些非常特殊的例子。然而,上述方法足以求解科学中常见的许多重要微分方程。
- 与微分不同,微分可以计算任何给定表达式的导数,许多表达式的积分不能用初等函数求。因此,不要浪费时间尝试集成无法集成的表达式。检查积分表以进行验证。不能用初等函数表示的微分方程的解有时可以用积分形式表示,但在这种情况下,积分是否可以解析进行并不重要。
- 发表于 2022-07-18 12:37
- 阅读 ( 36 )
- 分类:教育和通信
你可能感兴趣的文章
分子方程(molecular equation)和离子方程(ionic equation)的区别
分子方程和离子方程的关键区别在于,分子方程以分子形式表示反应物和产物,而离子方程则表示参与反应的离子物种。 化学反应是化合物之间的相互作用以形成新的化合物或重新排列它们的化学结构。经过某种化学反应的...
- 发布于 2020-10-16 16:52
- 阅读 ( 581 )
平衡方程(balanced equation)和净离子方程(net ionic equation)的区别
关键区别-平衡方程式与净离子方程式 所有的化学反应都可以写成一个方程式。这个方程的组成部分包括反应物及其物理状态,一个表示反应方向的箭头,以及反应与其物理状态的产物。如果使用了任何特殊条件,它们也会简...
- 发布于 2020-10-20 16:30
- 阅读 ( 737 )
代数表达式(algebraic expressions)和方程(equations)的区别
... •表达式可以计算给定值。 •由于上述事实,可以通过求解方程来找到未知量或变量。这些值被称为方程的解。 img.centered,.aligncenter{display:block;margin:0 auto 24px}.gallery-caption,.wp-caption-text{font-size:14px;font-size:1.4rem;font-weight:600;marg...
- 发布于 2020-10-22 23:59
- 阅读 ( 1741 )
线性的(linear)和非线性微分方程(nonlinear differential equations)的区别
线性与非线性微分方程 含有至少一个微分系数或未知变量导数的方程称为微分方程。微分方程可以是线性的也可以是非线性的。本文的范围是解释什么是线性微分方程,什么是非线性微分方程,线性微分方程和非线性微分方...
- 发布于 2020-10-25 06:59
- 阅读 ( 1618 )
不平等(inequalities)和方程(equations)的区别
...,显示它们是否大于或小于彼此,或者它们是否不相等。如何解决额外的一组解决方案非常复杂,需要进行评估。一个方程只需要简单的斜率和截距分析,这样就不那么复杂了。它的图在所有的方程中都有一条实线。一个由两个...
- 发布于 2021-06-23 14:25
- 阅读 ( 492 )
方程(equations)和功能(functions)的区别
...之间的差别变得模糊不清。这是因为两者都使用表达式来求解变量的值。再一次,这两个之间的差异是由它们的输出得出的。根据与表达式相等的值,公式可以有一个或两个变量值。另一方面,函数可以有基于变量值输入的解。...
- 发布于 2021-06-23 21:43
- 阅读 ( 490 )
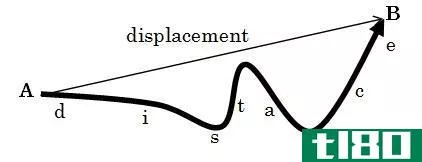
如何用运动方程解运动问题(solve motion problems using equations of motion)
...题,可以使用四个“suvat”方程。我们将看看这些方程是如何推导出来的,以及如何用它们来解决沿直线运动的物体的简单运动问题。 距离(distance)和取代(displacement)的区别 Distance is the total length of the path traveled by an object. This is a ...
- 发布于 2021-06-27 03:01
- 阅读 ( 254 )
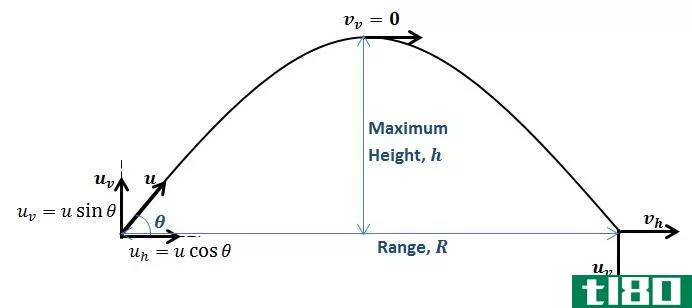
如何解决弹丸运动问题(solve projectile motion problems)
射弹是涉及二维的运动。为了解决弹丸运动问题,取两个相互垂直的方向(通常,我们使用“水平”和“垂直”方向),并将所有矢量(位移、速度、加速度)作为沿每个方向的分量。在弹丸中,垂直运动独立于水平运...
- 发布于 2021-06-27 03:02
- 阅读 ( 259 )
如何解决垂直圆周运动问题(solve vertical circular motion problems)
在本文中,我们将研究如何解决垂直圆周运动问题。解决这些问题的原理与解决向心加速度和向心力问题的原理相同。与水平圆不同的是,作用在垂直圆上的力随着它们的转动而变化。我们将考虑两种情况下物体在垂直...
- 发布于 2021-06-27 03:07
- 阅读 ( 413 )
差分放大器(differential amplifier)和运算放大器(operational amplifier)的区别
...阻抗和低输出阻抗的差分放大器。 什么是差分放大器(a differential amplifier)? A differential amplifier is an electric component which amplifies the difference between two signals applied to two input terminals, while rejecting signals which are common to both the input termina...
- 发布于 2021-06-27 08:19
- 阅读 ( 433 )