如何微分多项式(differentiate polynomials)

微分是微积分的基本过程之一。微分一个函数（通常称为f（x））会产生另一个称为导数的函数，写为f'（x）（“x的f素数”）。这个导数在物理和数学中有很多用途。例如，如果我们画一个多项式f（x），导数f’（x）告诉我们原始函数在所有点的斜率（变化率）。本文的第一部分教你区分多项式的每一项，一次一项。第二部分使用这种方法来处理一个典型的示例问题，即微分整个多项式。经过一些练习，微分5x3{\displa...

方法1方法1/2：微分多项式项

1将任何常数微分为零。常数是任何普通数字，不涉及任何变量，例如3、-16或2/3{\displaystyle 2/3}。在任何微分问题中，这些都是免费的，因为它们的导数总是0。划掉这个词，继续前进。用ddx（3）=0{\displaystyle{\frac{\mathrm{d}}}{\mathrm{d}x}（3）=0}的形式写这个。这表示“3对x的导数是0。”一个术语的导数是该术语的“变化率”：该术语在函数中变化的速度。因为常数永远不会改变（3将始终保持3），所以它的变化率始终为零。

Image titled Differentiate Polynomials Step 1

$2/3$

${\frac {\mathrm {d} }{\mathrm {d} x}}(3)=0$

2将x1{\displaystyle x^{1}区分为1。术语x1{\displaystyle x^{1}}（我们通常将其写成简单的x{\displaystyle x}）是另一个很容易区分的术语，只要您了解了规则。x{\displaystyle x}相对于x{\displaystyle x}的导数总是1。将其写成ddx（x）=1{\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}}（x）=1}。符号dx的意思是“相对于x的导数”。这意味着我们正在改变x的值，并观察其他项的响应变化是快还是慢。在ddx（x）{\displaystyle{\frac{\mathrm{d}}}{\mathrm{d}x}（x）}中，我们将x的变化与x的变化进行比较。这是同样的事情，这就是为什么变化率为1。

Image titled Differentiate Polynomials Step 2

$x^{1}$

${\frac {\mathrm {d} }{\mathrm {d} x}}(x)=1$

${\frac {\mathrm {d} }{\mathrm {d} x}}(x)$

3将x2{\displaystyle x^{2}的导数写成2x{\displaystyle 2x}。指数中的2在x前面移动，成为系数（该数字乘以x）同时，x2{\displaystyle x^{2}}被缩减为x{\displaystyle x}。你注意到一种模式了吗？在导数中，变量的指数值总是比原始项中的值低一个。x2{\displaystyle x^{2}}被“降级”为x1{\displaystyle x^{1}}（即x），x1{\displaystyle x^{1}}被“降级”为x0{\displaystyle x^{0}（等于1）。由于变量指数的值被称为多项式的“度”，我们可以说，对一个项进行微分会将该项的度减少一次。

Image titled Differentiate Polynomials Step 3

$x^{2}$

$x^{{2}}$

$x^{2}$

$x^{1}$

$x^{0}$

4微分xn{\displaystyle x^{n}}得到nxn−1{\displaystyle nx^{n-1}。或者在英语中：要区分一个被提升为指数的变量x，将该指数作为系数写在x前面，然后将指数减少1。这是最有用的区分规则之一。上面推导x2{\displaystyle x^{2}和x{\displaystyle x}的规则实际上只是这个一般规则的具体例子。示例：什么是ddx（x7）{\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}}（x^{7}}）（x7{\displaystyle x^{7}对x的导数）？指数7变成了项前面的系数：7x？{\displaystyle 7x^{？}新指数比原指数低一，7-1=6。答案是7x6{\displaystyle 7x^{6}。

Image titled Differentiate Polynomials Step 4

$x^{n}$

$nx^{n-1}$

$x^{2}$

${\frac {\mathrm {d} }{\mathrm {d} x}}(x^{7})$

$x^{7}$

$7x^{?}$

$7x^{6}$

5乘以原始项的系数。当你区分这个术语时，变量前面的系数不会改变。如果你的答案中有不止一个系数，把它们相乘。示例：什么是ddx（5x3）{\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}（5x^{3}}）？ddx（5x3）=5×ddx（x3）{\displaystyle{\frac{\mathrm{d}}}{\mathrm{d}x}（5x^{3}）=5乘以{\frac{\mathrm{d}{\mathrm{d}x}（x^{3}）（这意味着我们可以找到x3{\displaystyle x^{3}的导数，然后将我们的答案乘以5。）3）使指数3成为一个系数，然后减少指数1：ddx（3 3）3=3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3}=5乘以3x^{2}=15x^{2}

Image titled Differentiate Polynomials Step 5

${\frac {\mathrm {d} }{\mathrm {d} x}}(5x^{3})$

${\frac {\mathrm {d} }{\mathrm {d} x}}(5x^{3})=5\times {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})$

$x^{3}$

${\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})=3x^{2}$

$5\times {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})=5\times 3x^{2}=15x^{2}$

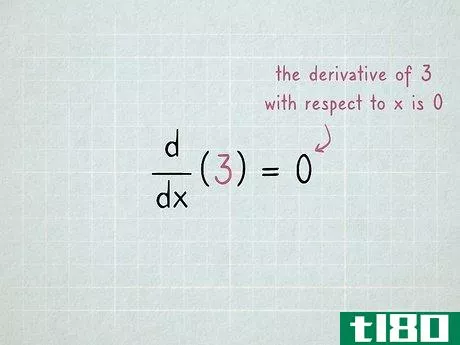
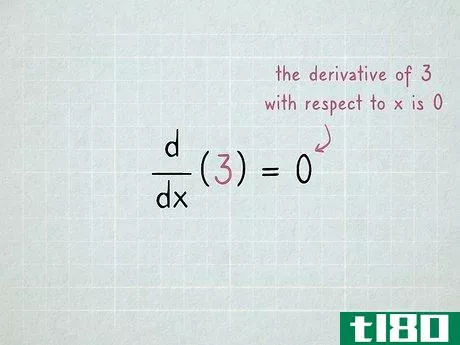
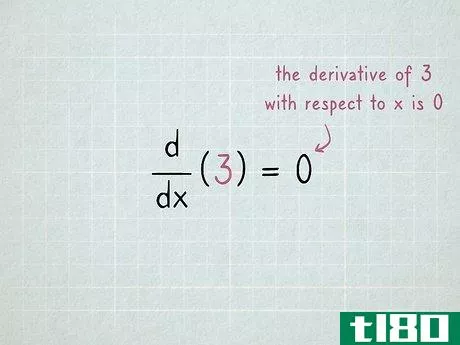
方法2方法2/2：微分整多项式

1将每个术语作为单独的问题处理。多项式包含多个加或减的项。要区分多项式，请分别区分每个项。可以不使用所有的加减符号。例如，以f（x）为例=−12x3+x2−5x+6{\displaystyle f（x）=-12x^{3}+x^{2}-5x+6}。导数f′（x）{\displaystyle f′（x）}等于每个项的导数，加或减与原始项相同。用数学术语，我们可以这样写：ddx（f（x））=ddx(−12x3+x2−5x+6）{\displaystyle{\frac{\mathrm{d}}}{\mathrm{d}x}（f（x））={\frac{\mathrm{d}}{\mathrm{d}x}（-12x^{3}+x^{2}-5x+6}=ddx(−12x3）+ddx（x2）−ddx（5x）+ddx（6）{\displaystyle={\frac{\mathrm{d}}{\mathrm{d}x}（-12x{3}）+{\frac{\mathrm{d}}{\mathrm{d}}{\mathrm{d}x}（x^{2}）{\frac{\mathrm{d}{d}{x}（5x}+frac{\mathrm{d}{d}。

Image titled Differentiate Polynomials Step 6

$f(x)=-12x^{3}+x^{2}-5x+6$

${\frac {\mathrm {d} }{\mathrm {d} x}}(f(x))={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3}+x^{2}-5x+6)$

$={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3})+{\frac {\mathrm {d} }{\mathrm {d} x}}(x^{2})-{\frac {\mathrm {d} }{\mathrm {d} x}}(5x)+{\frac {\mathrm {d} }{\mathrm {d} x}}(6)$

2去掉常数项。如果有一个常数（一个没有变量的项），删除它。微分总是去掉常数项。在我们的例子中，6是常数。ddx（6）=0{\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}（6）=0}，所以我们可以去掉它。注意：只有不带变量的项才是常量。此规则不影响乘以x或任何其他变量的数字。

Image titled Differentiate Polynomials Step 7

${\frac {\mathrm {d} }{\mathrm {d} x}}(6)=0$

3将每个变量的指数移到术语的前面。记住，当我们微分时，每个变量的指数都变成了一个系数。如果项前面已经有一个系数，将两个系数相乘。f′（x）=ddx(−12x3）+ddx（x2）−ddx（5x）{\displaystyle f'（x）={\frac{\mathrm{d}}{\mathrm{d}x}（-12x{3}）+{\frac{\mathrm{d}}{\mathrm{d}}{\mathrm{d}x}（x^{2}）{\frac{\mathrm{d}{d}{x}（5x}）−12） x+2倍？−（1×5）x？{\displaystyle=（3次-12）x^{？}+2x^{？}-（1乘以5）x ^{？}=−36x+2倍？−5倍？{\displaystyle=-36x^{？}+2x^{？}-5x^{？}由于x=x1{\displaystyle x=x^{1}，我们取“1”指数，并将其移动到5x{\displaystyle 5x}项前面。因为乘以1永远不会改变这个术语，一旦你明白了发生了什么，你就可以跳过这一步。

Image titled Differentiate Polynomials Step 8

$f'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3})+{\frac {\mathrm {d} }{\mathrm {d} x}}(x^{2})-{\frac {\mathrm {d} }{\mathrm {d} x}}(5x)$

$=(3\times -12)x^{?}+2x^{?}-(1\times 5)x^{?}$

$=-36x^{?}+2x^{?}-5x^{?}$

$x=x^{1}$

4将每个指数降低一度。为此，从每个变量项的每个指数中减去1。f′（x）=−36x3−1+2x2−1.−5x1−1{\displaystyle f'（x）=-36x^{3-1}+2x^{2-1}-5x^{1-1}=−36x2+2x1−5x0{\displaystyle=-36x^{2}+2x^{1}-5x^{0}=−36x2+2x−5{\displaystyle=-36x^{2}+2x-5}记住x1{\displaystyle x^{1}}与x{\displaystyle x}相同。还要记住，任何提升到零次方（x0{\displaystyle x^{0}}）的值都等于1。

Image titled Differentiate Polynomials Step 9

$f'(x)=-36x^{3-1}+2x^{2-1}-5x^{1-1}$

$=-36x^{2}+2x^{1}-5x^{0}$

$=-36x^{2}+2x-5$

$x^{{1}}$

$x^{{0}}$

5在给定的“x”值下求出新方程的值。您已经完成了差异化，但在测试问题中有一个常见的下一步。如果你被要求“计算表达式”中的x值，你所需要做的就是用给定的值替换新方程中的每个x并求解。例如，计算x=2时的导数f'（x）。我们发现的微分方程是f′（x）=−36x2+2x−5{\displaystyle f'（x）=-36x^{2}+2x-5}f′（2）=−36(2)2+2(2)−5{\displaystyle f'（2）=-36（2）^{2}+2（2）-5}=−36(4)+4−5{\displaystyle=-36（4）+4-5}=−144+4−5{\displaystyle=-144+4-5}=−145{\displaystyle=-145}这个答案与原始函数f（x）有关。它告诉我们，如果我们在x=2处画一条切线，那条切线的斜率是-145。

Image titled Differentiate Polynomials Step 10

$f'(x)=-36x^{2}+2x-5$

$f'(2)=-36(2)^{2}+2(2)-5$

$=-36(4)+4-5$

$=-144+4-5$

$=-145$

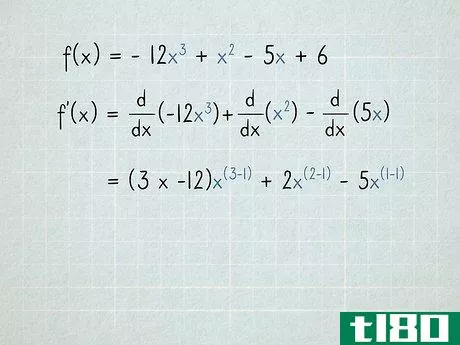
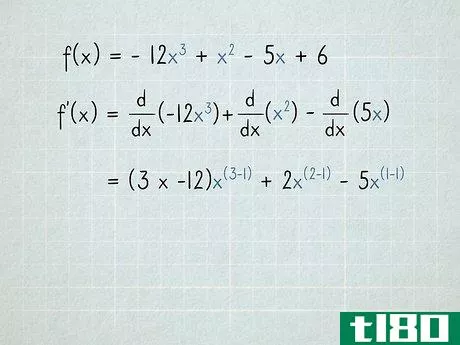
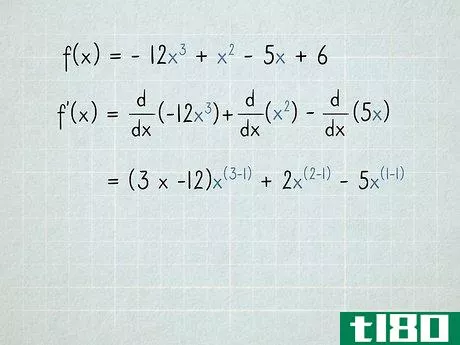
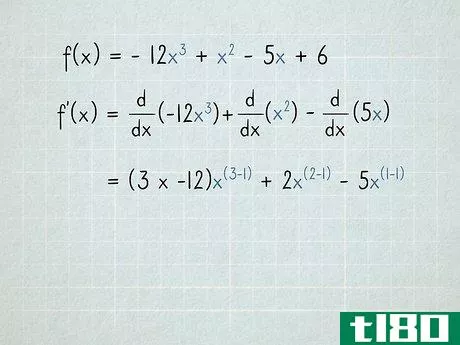
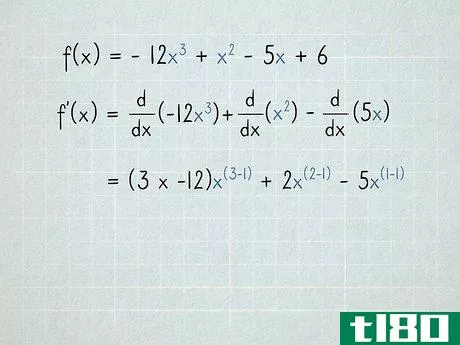
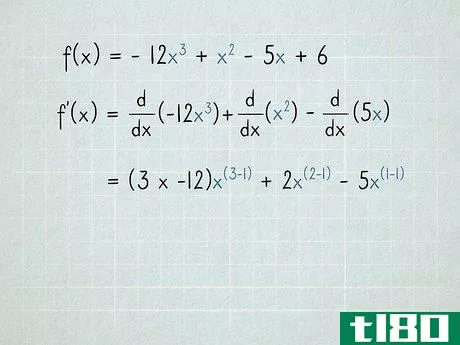
额外棘手的问题可能包括变为负指数或分数指数的变量。这些函数在技术上不是多项式，但你可以用同样的规则来区分它们。仔细工作，确保从负指数中正确减去。例如，ddx（7x−4） {\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}}（7x^{-4}）=(−4×7）x−4.−1{\displaystyle=（-4乘以7）x^{-4-1}=−28x−5{\displaystyle=-28x^{-5}。

发表于 2022-03-22 16:00
阅读 ( 96 )
分类：教育

你可能感兴趣的文章

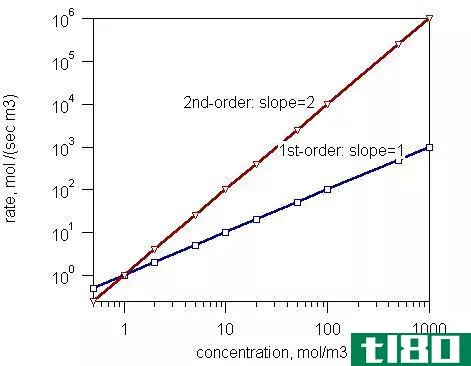
微分速率定律(differential rate law)和综合费率法(integrated rate law)的区别

...法与综合汇率法的表格形式 6. 摘要什么是微分速率定律(differential rate law)？微分速率定律用于确定一个化学反应的速率，它是一个或多个反应物在特定时间段内浓度变化的函数。微分速率定律表明在化学反应的分子水平上发生...

发布于 2020-10-16 09:23
阅读 ( 1227 )

线性的(linear)和非线性微分方程(nonlinear differential equations)的区别

...程之间的差异是很重要的。什么是线性微分方程(a linear differential equation)？假设f:X→Y和f（X）=Y，一个没有未知函数Y及其导数的非线性项的微分方程称为线性微分方程。它规定了一个条件，即y不能有更高的指数项，如y2，y3，...

发布于 2020-10-25 06:59
阅读 ( 1612 )

$\\frac{df}{d\\boldsymbol{u}}=\\lim_{h \to 0}\\frac{f(\\boldsymbol{x}+h \\boldsymbol{u})-f(\\boldsymbol{x})}{h}$

导数(derivative)和有差别的(differential)的区别

...he well-known definition of the derivative, For example, is everywhere differentiable, and the derivative is equal to the limit, , which is equal to . The derivatives of functi*** such as exist everywhere. They are respectively equal to the functi*** . ...

发布于 2020-10-25 13:25
阅读 ( 606 )

$\\frac{df}{d\\boldsymbol{u}}=\\lim_{h \to 0}\\frac{f(\\boldsymbol{x}+h \\boldsymbol{u})-f(\\boldsymbol{x})}{h}$

区别(differentiation)和导数(derivative)的区别

发布于 2020-10-26 13:11
阅读 ( 624 )

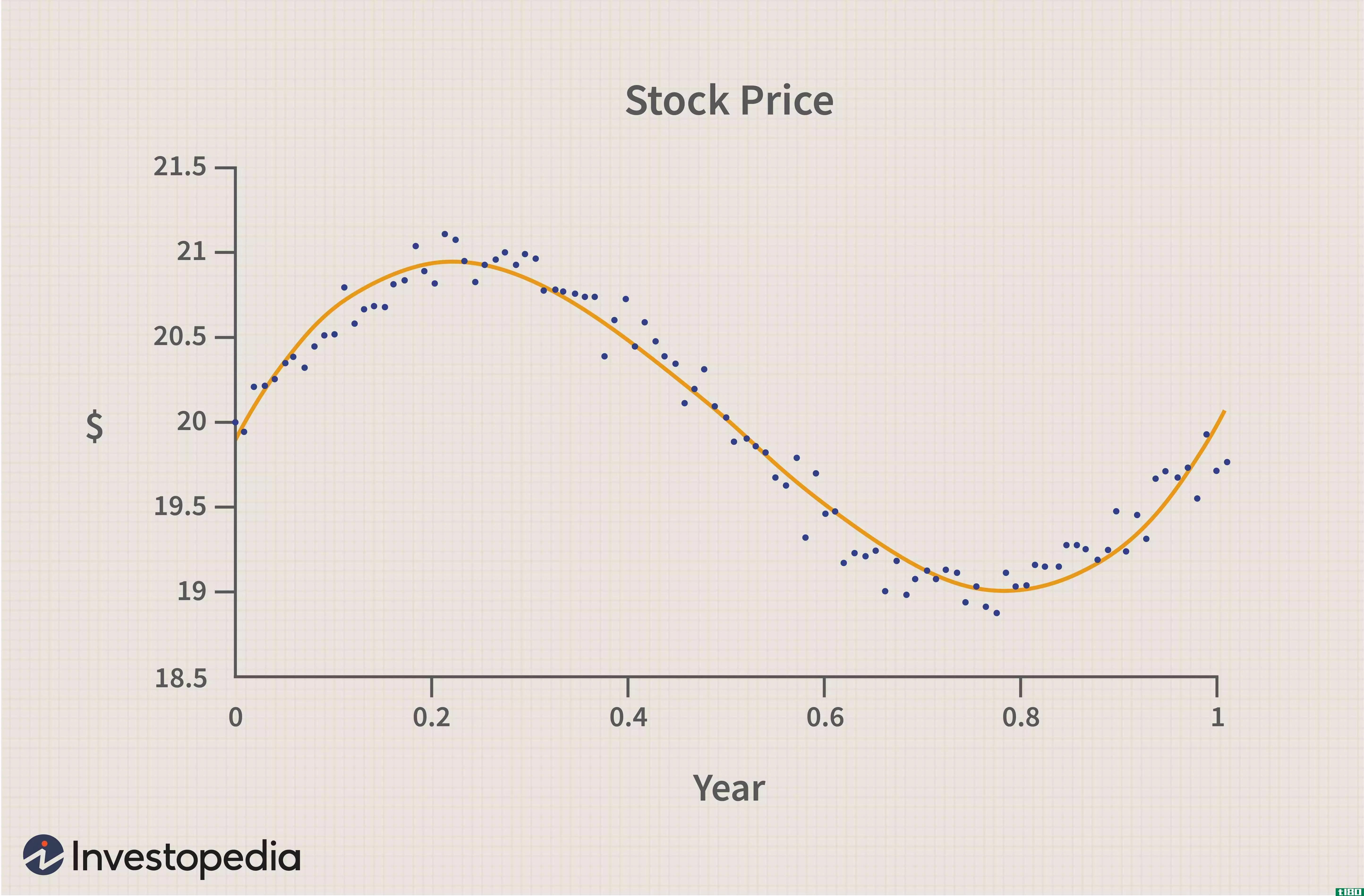
多项式趋势定义

什么是多项式趋势(polynomial trending)？多项式趋势描述了数据中的一种模式，这种模式是弯曲的或从直线趋势中断的。它经常发生在包含许多波动的大量数据中。随着更多的数据可用，趋势往往变得不那么线性，多项式趋势取而...

发布于 2021-06-04 00:42
阅读 ( 246 )

区别(differentiation)和集成(integration)的区别

...括学生和学者都未能突出差异和整合。什么是区别(differentiation)？微分是微积分中的一个术语，指的是与另一个相关性质的单位变化有关的性质的变化。在另一个术语中，微分形成一个代数表达式，有助于计算曲线在给定...

发布于 2021-06-25 05:40
阅读 ( 418 )

有差别的(differential)和导数(derivative)的区别

...支之一。另一个分支叫做积分学。什么是有差别的(differential)？微分学和积分学是微积分学的基础分支之一。它是微积分的一个子领域，处理一些变化量的无穷小变化。我们生活的世界充满了周期性变化的相互关联的量。 ...

发布于 2021-06-25 20:02
阅读 ( 449 )

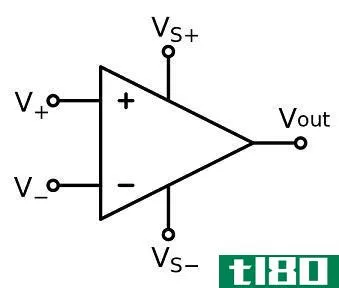
差分放大器(differential amplifier)和运算放大器(operational amplifier)的区别

...阻抗和低输出阻抗的差分放大器。什么是差分放大器(a differential amplifier)？ A differential amplifier is an electric component which amplifies the difference between two signals applied to two input terminals, while rejecting signals which are common to both the input termina...

发布于 2021-06-27 08:19
阅读 ( 429 )

选择性(selective)和微分介质(differential media)的区别

主要差异选择(main difference selective) vs. 微分介质(differential media) 选择性培养基和差异培养基是分离鉴定微生物的两种培养基。选择性培养基和差异培养基的主要区别在于选择性培养基用于分离特定的微生物菌株，而差异...

发布于 2021-06-30 12:14
阅读 ( 386 )

区别(differentiation)和集成(integration)的区别

...的区别。许多学生甚至学者都无法理解它的区别。区别(differentiation) vs. 集成(integration)微分法和积分法的区别在于微分法是用来找出曲线的瞬时变化率和斜率的，而如果你需要计算曲线下的面积，那么就利用积分法。如你所见，...

发布于 2021-07-09 23:13
阅读 ( 230 )